 είναι ο εγγεγραμμένος κύκλος ισοσκελούς τριγώνου
είναι ο εγγεγραμμένος κύκλος ισοσκελούς τριγώνου 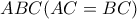 και
και  ο κύκλος
ο κύκλος που εφάπτεται στις
 και εξωτερικά στον κύκλο
και εξωτερικά στον κύκλο  Nα υπολογίσετε συναρτήσει του
Nα υπολογίσετε συναρτήσει του  τον λόγο
τον λόγο 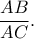 Για ποια
Για ποιατιμή του
 το τρίγωνο
το τρίγωνο  είναι ισόπλευρο;
είναι ισόπλευρο;Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 είναι ο εγγεγραμμένος κύκλος ισοσκελούς τριγώνου
είναι ο εγγεγραμμένος κύκλος ισοσκελούς τριγώνου 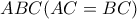 και
και  ο κύκλος
ο κύκλος  και εξωτερικά στον κύκλο
και εξωτερικά στον κύκλο  Nα υπολογίσετε συναρτήσει του
Nα υπολογίσετε συναρτήσει του  τον λόγο
τον λόγο 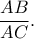 Για ποια
Για ποια το τρίγωνο
το τρίγωνο  είναι ισόπλευρο;
είναι ισόπλευρο;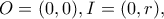 και προβάλλοντας το
και προβάλλοντας το  επί της
επί της  στο
στο  λαμβάνουμε από
λαμβάνουμε από  και Πυθαγόρειο Θεώρημα
και Πυθαγόρειο Θεώρημα  οπότε
οπότε 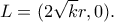 Εύκολα προκύπτει η εξίσωση της
Εύκολα προκύπτει η εξίσωση της  ,
,  και η τομή της με την
και η τομή της με την 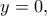

 της
της  χωρίς να γνωρίζουμε (ακόμη) τις συντεταγμένες των
χωρίς να γνωρίζουμε (ακόμη) τις συντεταγμένες των  Κείμενο επί της
Κείμενο επί της  το
το  είναι της μορφής
είναι της μορφής  Το
Το  προσδιορίζεται από την
προσδιορίζεται από την 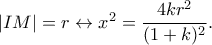 Επειδή το
Επειδή το  κείται αριστερά της
κείται αριστερά της 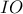 ισχύει η
ισχύει η 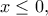 οπότε επιλέγουμε την αρνητική ρίζα για να λάβουμε
οπότε επιλέγουμε την αρνητική ρίζα για να λάβουμε 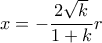 και
και 
 και η
και η 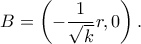 Και βέβαια, από τις συντεταγμένες των
Και βέβαια, από τις συντεταγμένες των  και
και  προκύπτει άμεσα και η
προκύπτει άμεσα και η 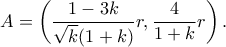
 είναι ισόπλευρο αν και μόνον αν το
είναι ισόπλευρο αν και μόνον αν το  κείται επί της
κείται επί της 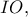 όταν δηλαδή
όταν δηλαδή 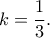 Εύκολα υπολογίζονται και τα μήκη
Εύκολα υπολογίζονται και τα μήκη 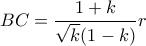 και
και 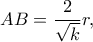 και επαληθεύεται η
και επαληθεύεται η  .
.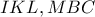 είναι
είναι 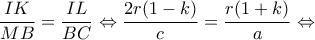

 οπότε
οπότε 
 μέχρι το
μέχρι το  -- και για τον υπολογισμό του αθροίσματος γεωμετρικής σειράς, καθότι
-- και για τον υπολογισμό του αθροίσματος γεωμετρικής σειράς, καθότι 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες