 είναι το μέσο του ημικυκλίου διαμέτρου
είναι το μέσο του ημικυκλίου διαμέτρου  . Σχεδιάζω ημικύκλιο διαμέτρου
. Σχεδιάζω ημικύκλιο διαμέτρου 
και ένα τρίτο ημικύκλιο , κέντρου
 , το οποίο εφάπτεται στο δεύτερο , έχει τα άκρα του
, το οποίο εφάπτεται στο δεύτερο , έχει τα άκρα του  και
και  στην
στην ευθεία
 και τέμνει το αρχικό στο σημείο
και τέμνει το αρχικό στο σημείο  . Υπολογίστε το τμήμα
. Υπολογίστε το τμήμα  και την γωνία :
και την γωνία :  .
.
 . Έστω ακόμα
. Έστω ακόμα  το σημείο επαφής των κόκκινου( κέντρου
το σημείο επαφής των κόκκινου( κέντρου  ) και πράσινου( κέντρου
) και πράσινου( κέντρου  , Δηλαδή η ακτίνα του πράσινου ημικυκλίου είναι
, Δηλαδή η ακτίνα του πράσινου ημικυκλίου είναι  .
.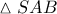 , έχω :
, έχω :  . Δηλαδή ,
. Δηλαδή ,  .
.
 . Είναι
. Είναι  . Άρα
. Άρα  .
. έχω:
έχω: 