 πλευράς
πλευράς  και το ημικύκλιο διαμέτρου
και το ημικύκλιο διαμέτρου  εκτός του τετραγώνου. Να βρείτε τη θέση
εκτός του τετραγώνου. Να βρείτε τη θέση σημείου
 στο ημικύκλιο για την οποία μεγιστοποιείται το
στο ημικύκλιο για την οποία μεγιστοποιείται το  καθώς και τη μέγιστη τιμή του αθροίσματος.
καθώς και τη μέγιστη τιμή του αθροίσματος.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 πλευράς
πλευράς  και το ημικύκλιο διαμέτρου
και το ημικύκλιο διαμέτρου  εκτός του τετραγώνου. Να βρείτε τη θέση
εκτός του τετραγώνου. Να βρείτε τη θέση  στο ημικύκλιο για την οποία μεγιστοποιείται το
στο ημικύκλιο για την οποία μεγιστοποιείται το  καθώς και τη μέγιστη τιμή του αθροίσματος.
καθώς και τη μέγιστη τιμή του αθροίσματος. ,
,  , για
, για  .
. Θανάση, έτσι κι αλλιώς το
 είναι ρητός για οποιαδήποτε τιμή της πλευράς
είναι ρητός για οποιαδήποτε τιμή της πλευράς  του τετραγώνου.
Η λύση μου είναι παρόμοια μόνο που έχω πάρει
του τετραγώνου.
Η λύση μου είναι παρόμοια μόνο που έχω πάρει  και καταλήγω στη μελέτη της συνάρτησης
και καταλήγω στη μελέτη της συνάρτησης που δίνει για
που δίνει για  μέγιστο
μέγιστο 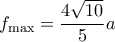
 για να βγει το
για να βγει το  ακέραιος κ.λπ. Εσύ Θανάση, έθεσες
ακέραιος κ.λπ. Εσύ Θανάση, έθεσες  που δίνει
που δίνει 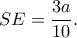
 γίνεται με την τομή του ημικυκλίου με το Απολλώνιο κύκλο που για κάθε σημείο του
γίνεται με την τομή του ημικυκλίου με το Απολλώνιο κύκλο που για κάθε σημείο του  ,
,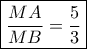
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες