 , έχει σταθερή υποτείνουσα
, έχει σταθερή υποτείνουσα  και μεταβλητές τις κάθετες πλευρές .
και μεταβλητές τις κάθετες πλευρές .Στην προέκταση της
 , θεωρούμε σημείο
, θεωρούμε σημείο  , τέτοιο ώστε :
, τέτοιο ώστε :  . Βρείτε το
. Βρείτε το  .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , έχει σταθερή υποτείνουσα
, έχει σταθερή υποτείνουσα  και μεταβλητές τις κάθετες πλευρές .
και μεταβλητές τις κάθετες πλευρές . , θεωρούμε σημείο
, θεωρούμε σημείο  , τέτοιο ώστε :
, τέτοιο ώστε :  . Βρείτε το
. Βρείτε το  .
.Από το ορθογώνιο τρίγωνο
 έχουμε
έχουμε 

 , με σύνολό τιμών της μεταβλητής το
, με σύνολό τιμών της μεταβλητής το  (το
(το  είναι σταθερό). Η παραπάνω έχει παράγωγο (ως προς
είναι σταθερό). Η παραπάνω έχει παράγωγο (ως προς  ) την
) την  .
. (άμεσο), από όπου με αντικατάσταση η μέγιστη τιμή του
(άμεσο), από όπου με αντικατάσταση η μέγιστη τιμή του  (το αφήνω ως ανιαρές πράξεις ρουτίνας).
(το αφήνω ως ανιαρές πράξεις ρουτίνας).Καλησπέρα σε όλους. Θέλω να μοιραστώ με τους γεωμέτρες μας μια εικασία: Το μέγιστο εμφανίζεται όταν τα τρίγωνα
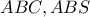 είναι όμοια.
είναι όμοια.

![\displaystyle \eta {\mu ^2}C + \eta \mu 2C,\;\;C \in \left[ {0,\frac{\pi }{2}} \right] \displaystyle \eta {\mu ^2}C + \eta \mu 2C,\;\;C \in \left[ {0,\frac{\pi }{2}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/61b61b86cba85edfd0dec1a08947c6c6.png) (Παρακάτω θα γίνει κατανοητό γιατί πήραμε και τα άκρα του διαστήματος).
(Παρακάτω θα γίνει κατανοητό γιατί πήραμε και τα άκρα του διαστήματος).

 και για
και για  .
. , που σημαίνει ότι τα τρίγωνα
, που σημαίνει ότι τα τρίγωνα 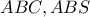 είναι όμοια.
είναι όμοια.Εύκολα βλέπουμε ότι ο γεωμετρικός τόπος τουΓιώργος Ρίζος έγραψε: ↑Κυρ Νοέμ 30, 2025 9:43 pmΕπειδή εμπλέκεται η χρυσή τομή πιστεύω ότι θα βρεθεί και γεωμετρική προσέγγιση.
 είναι το μοβ ημικύκλιο . Προφανώς το μέγιστο του
είναι το μοβ ημικύκλιο . Προφανώς το μέγιστο του 
 και ισούται με
και ισούται με  . Είναι ανεστραμμένη η γνωστή κατασκευή του
. Είναι ανεστραμμένη η γνωστή κατασκευή του  !
!Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες