 .
.Β) Τμήμα
 , μήκους
, μήκους  , ολισθαίνει έχοντας τα άκρα του στις ευθείες
, ολισθαίνει έχοντας τα άκρα του στις ευθείες 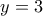 και
και  .
.Υπολογίστε - με δύο τουλάχιστον τρόπους - το ελάχιστο της διαδρομής :
 .
. .
. , μήκους
, μήκους  , ολισθαίνει έχοντας τα άκρα του στις ευθείες
, ολισθαίνει έχοντας τα άκρα του στις ευθείες 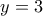 και
και  .
. .
.Ας δώσω αλγεβρική λύση αλλά υπάρχει και ωραία γεωμετρική.
 . Υψώνοντας στο τετράγωνο είναι
. Υψώνοντας στο τετράγωνο είναι ![(x-4)^2 [(x-2)^2+16]=(x-2)^2[(x-4)^2+4] (x-4)^2 [(x-2)^2+16]=(x-2)^2[(x-4)^2+4]](/forum/ext/geomar/texintegr/latexrender/pictures/87d2a8810b1c5e6ff4868f8f7ec62191.png) , άρα
, άρα  από όπου (με διάφορους τρόπους)
από όπου (με διάφορους τρόπους)  ή
ή 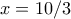 . Με έλεγχο στην αρχική, κτατάμε την δεύτερη.
. Με έλεγχο στην αρχική, κτατάμε την δεύτερη. , το
, το 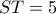 δίνει
δίνει 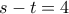 . Και θέλουμε το ελάχιστο του
. Και θέλουμε το ελάχιστο του  ή αλλιώς του
ή αλλιώς του 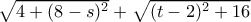 .
.  η παράσταση αυτή γράφεται
η παράσταση αυτή γράφεται  .
.  . Αλλά αυτή ισοδυναμεί με την εξίσωση στο α). Τα υπόλοιπα είναι ρουτίνα.
. Αλλά αυτή ισοδυναμεί με την εξίσωση στο α). Τα υπόλοιπα είναι ρουτίνα. με παράλληλη μετατόπιση στην θέση
με παράλληλη μετατόπιση στην θέση  , οπότε σχηματίζεται ένα παραλληλόγραμμο
, οπότε σχηματίζεται ένα παραλληλόγραμμο  του οποίου οι κορυφές
του οποίου οι κορυφές  είναι δεδομένες. Επειδή
είναι δεδομένες. Επειδή 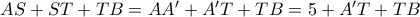 , το πρόβλημά μας ανάγεται στην εύρεση της ελάχιστης διαδρομής
, το πρόβλημά μας ανάγεται στην εύρεση της ελάχιστης διαδρομής  . Αλλά αυτή είναι η ευθεία
. Αλλά αυτή είναι η ευθεία  .
.Αλλιώς για το Α) Αρχικά είναι
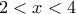 και
και 
 Κατασκευάζω ορθογώνιο τρίγωνο
Κατασκευάζω ορθογώνιο τρίγωνο  με κάθετες πλευρές
με κάθετες πλευρές  και έστω
και έστω  το μέσο του
το μέσο του  και
και σημείο της πλευράς
σημείο της πλευράς  ώστε
ώστε  Προφανώς,
Προφανώς, 
 προκύπτει ότι
προκύπτει ότι  άρα το
άρα το  είναι μέσο του
είναι μέσο του  οπότε
οπότε 
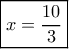
 , το πρόβλημα ισοδυναμεί
, το πρόβλημα ισοδυναμεί 
 και
και 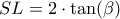 , άρα ζητάμε ελαχιστοποίηση για το
, άρα ζητάμε ελαχιστοποίηση για το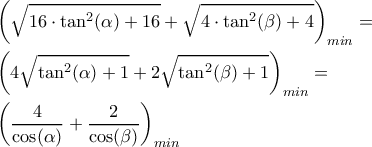

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες