Η γωνία με κορυφή το

είναι σταθερή και ίση, ως προς το μέτρο της, με την απόλυτη ημιδιαφορά των μέτρων των τόξων

, οπότε το τόξο

είναι σταθερό, άρα και η γωνία

, με μέτρο το ημιάθροισμα των μέτρων των τόξων

, είναι σταθερή. Επομένως, κ.λπ., ο γ.τ. του

είναι κύκλος.
Ας δούμε έναν τρόπο εύρεσης της εξίσωσής του.
Οι θέσεις του

στον οριζόντιο άξονα έχουν τετμημένες -5,5 και 2,5 (απλό).Οι πολικές τους, ως προς τον δεξιό κύκλο, είναι οι ευθείες με εξισώσεις (που θυμίζουν τις εξισώσεις των εφαπτομένων του, σαν να ήταν το S σημείο επαφής):

Τα σημεία που τέμνουν τον οριζόντιο άξονα είναι οι αντίστοιχες θέσεις του

, (το

ανήκει στην πολική του

), οι οποίες προφανώς είναι αντιδιαμετρικά σημεία του ζητούμενου κύκλου. Βρίσκουμε, εύκολα, τα σημεία αυτά και στη συνέχεια τον ζητούμενο κύκλο...
 είναι τα σημεία τομής των δύο κύκλων του σχήματος . Από κινητό σημείο
είναι τα σημεία τομής των δύο κύκλων του σχήματος . Από κινητό σημείο  του μικρού κύκλου ,
του μικρού κύκλου ,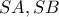 , οι οποίες ξανατέμνουν το μεγάλο στα σημεία
, οι οποίες ξανατέμνουν το μεγάλο στα σημεία  . Ονομάζουμε
. Ονομάζουμε  ,
, . Βρείτε την καρτεσιανή εξίσωση του γεωμετρικού τόπου του
. Βρείτε την καρτεσιανή εξίσωση του γεωμετρικού τόπου του  .
. είναι σταθερή και ίση, ως προς το μέτρο της, με την απόλυτη ημιδιαφορά των μέτρων των τόξων
είναι σταθερή και ίση, ως προς το μέτρο της, με την απόλυτη ημιδιαφορά των μέτρων των τόξων  , οπότε το τόξο
, οπότε το τόξο  είναι σταθερό, άρα και η γωνία
είναι σταθερό, άρα και η γωνία  , με μέτρο το ημιάθροισμα των μέτρων των τόξων
, με μέτρο το ημιάθροισμα των μέτρων των τόξων 
 ανήκει στην πολική του
ανήκει στην πολική του  και
και  . Ο κύκλος με διάμετρο
. Ο κύκλος με διάμετρο  είναι
είναι  .
.