 κινείται σε ημικύκλιο διαμέτρου
κινείται σε ημικύκλιο διαμέτρου  και
και  είναι η προβολή του στη διάμετρο .
είναι η προβολή του στη διάμετρο .Υπολογίστε τη μέγιστη τιμή του γινομένου :
 ...
...  ώρες , μόνο για μαθητές .
ώρες , μόνο για μαθητές . κινείται σε ημικύκλιο διαμέτρου
κινείται σε ημικύκλιο διαμέτρου  και
και  είναι η προβολή του στη διάμετρο .
είναι η προβολή του στη διάμετρο . ...
...  ώρες , μόνο για μαθητές .
ώρες , μόνο για μαθητές .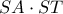 παρουσιάζει μέγιστο όταν και το
παρουσιάζει μέγιστο όταν και το  παρουσιάζει μέγιστο.
παρουσιάζει μέγιστο. είναι
είναι  και
και  .
. , σταθερό και
, σταθερό και 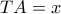 ,
,  .
.
![\displaystyle f\left( x \right) = - {x^3} + {a^2}{x^2},\;\;x \in \left[ {0,\;a} \right] \displaystyle f\left( x \right) = - {x^3} + {a^2}{x^2},\;\;x \in \left[ {0,\;a} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/32d7094054ecf2ba56ace3836b77fe00.png) έχει παράγωγο
έχει παράγωγο  .
. .
.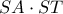 παρουσιάζεται όταν
παρουσιάζεται όταν  και ισούται με
και ισούται με  .
. 
 , σταθερό, το γινόμενο των θετικών παραγόντων
, σταθερό, το γινόμενο των θετικών παραγόντων  γίνεται μέγιστο όταν
γίνεται μέγιστο όταν  και συνεχίζουμε, όπως παραπάνω.
και συνεχίζουμε, όπως παραπάνω. είναι
είναι  .
. ,
,  .
. , σταθερό και
, σταθερό και 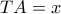 ,
,  .
. .
.  παρουσιάζει μέγιστο για
παρουσιάζει μέγιστο για  με μέγιστη τιμή
με μέγιστη τιμή  .
. με το μέγιστο όταν
με το μέγιστο όταν  . Τότε, όμως, έχουμε προφανώς την ακραία περίπτωση όπου το
. Τότε, όμως, έχουμε προφανώς την ακραία περίπτωση όπου το  ταυτίζεται με το
ταυτίζεται με το  , οπότε έχουμε ελάχιστο, το
, οπότε έχουμε ελάχιστο, το  .
. Επαναφέρω το ερώτημα για την αναζήτηση του λάθους στην παραπάνω "απόδειξη". Αν και δεν υπήρχε ανταπόκριση εξακολουθώ να πιστεύω ότι πρόκειται για ένα πολύ κρίσιμο σημείο στη διδασκαλία μας, παρόλο που το βασικό πεδίο εφαρμογής του (γεωμετρία μιγαδικών) είναι πια εκτός ύλης.Γιώργος Ρίζος έγραψε: ↑Παρ Ιουν 22, 2018 5:27 pm
(*) Ας περιμένουμε λίγο (μία - δύο) μέρες απαντήσεις μαθητών και κατόπιν ας συμμετέχει όποιος επιθυμεί.
 . Τότε η εξίσωση του ημικυκλίου είναι
. Τότε η εξίσωση του ημικυκλίου είναι 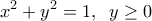 , οπότε
, οπότε  .
.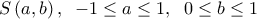 με
με  , οπότε
, οπότε  .
.
![\displaystyle f\left( x \right) = - {x^3} - {x^2} + x + 1,\;\;x \in \left[ { - 1,\;1} \right] \displaystyle f\left( x \right) = - {x^3} - {x^2} + x + 1,\;\;x \in \left[ { - 1,\;1} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/568f4d4f034ae587fac1f8bd3dc65f50.png)
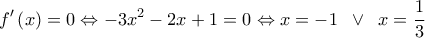
 βρίσκουμε ότι η
βρίσκουμε ότι η  παρουσιάζει μέγιστο για
παρουσιάζει μέγιστο για  (κι εννοείται ελάχιστο για
(κι εννοείται ελάχιστο για  ή
ή  ).
).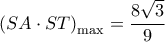 και αφού
και αφού  , θα είναι
, θα είναι 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες