Έστω ότι τα σημεία
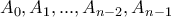 διαιρούν το μοναδιαίο κύκλο σε
διαιρούν το μοναδιαίο κύκλο σε  ίσα τμήματα. Να υπολογίσετε το γινόμενο
ίσα τμήματα. Να υπολογίσετε το γινόμενο
Προσπαθήστε με χρήση μιγαδικών ή αλλο τρόπο να υπολογίσετε το γινόμενο ανεξάρτητα από τα αποτελέσματα στην παραπομπή.
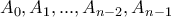 διαιρούν το μοναδιαίο κύκλο σε
διαιρούν το μοναδιαίο κύκλο σε  ίσα τμήματα. Να υπολογίσετε το γινόμενο
ίσα τμήματα. Να υπολογίσετε το γινόμενο

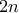 ίσα τμήματα.
ίσα τμήματα. 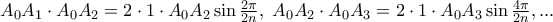 , οπότε με πολλαπλασιασμό κατά μέλη και λαμβάνοντας υπόψη ότι
, οπότε με πολλαπλασιασμό κατά μέλη και λαμβάνοντας υπόψη ότι  ή
ή  παίρνουμε για
παίρνουμε για  το ζητούμενο γινόμενο...
το ζητούμενο γινόμενο...Καλησπέρα. Μια προσπάθεια ... Στην περίπτωσή μας έχουμε τις νιοστές ρίζες της μονάδας. Ωραίες αναμνήσεις από μιγαδικούς σε τριγωνομετρική μορφή...Al.Koutsouridis έγραψε: ↑Κυρ Ιούλ 08, 2018 1:48 pmΜε αφορμή το πρόβλημα του Ορέστη εδώ και δεδομένου των απαντήσεων και των τύπων που δόθηκαν.
Έστω ότι τα σημείαδιαιρούν το μοναδιαίο κύκλο σε
ίσα τμήματα. Να υπολογίσετε το γινόμενο
enkuklo_ginomeno.png
Προσπαθήστε με χρήση μιγαδικών ή αλλο τρόπο να υπολογίσετε το γινόμενο ανεξάρτητα από τα αποτελέσματα στην παραπομπή.
 , με
, με 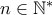 έχει ακριβώς
έχει ακριβώς  διαφορετικές ρίζες, οι οποίες δίνονται από τον τύπο:
διαφορετικές ρίζες, οι οποίες δίνονται από τον τύπο: .
. των αντίστοιχων λύσεων της εξίσωσης
των αντίστοιχων λύσεων της εξίσωσης  είναι κορυφές κανονικού πολυγώνου με
είναι κορυφές κανονικού πολυγώνου με  πλευρές εγγεγραμμένου σε κύκλο με κέντρο
πλευρές εγγεγραμμένου σε κύκλο με κέντρο  και ακτίνα
και ακτίνα  .
.
 .
.

 .
.δεν υπήρχε περίπτωση να φτάσω εδώ. Ευχαριστώ πολύ για την Άσκηση!Al.Koutsouridis έγραψε: ↑Κυρ Ιούλ 08, 2018 1:48 pmΜε αφορμή το πρόβλημα του Ορέστη εδώ και δεδομένου των απαντήσεων και των τύπων που δόθηκαν.
.......
Προσπαθήστε με χρήση μιγαδικών ή αλλο τρόπο να υπολογίσετε το γινόμενο ανεξάρτητα από τα αποτελέσματα στην παραπομπή.
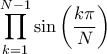 . Απλά χρειάζεται να
. Απλά χρειάζεται να  στον μοναδιαίο κύκλο είναι
στον μοναδιαίο κύκλο είναι  .
. 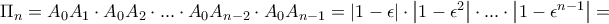

 οι ρίζες της μονάδας που αντιστοιχούν στα σημεία
οι ρίζες της μονάδας που αντιστοιχούν στα σημεία 
 ,
,  βαθμού. Το ζητούμενο γινόμενο είναι
βαθμού. Το ζητούμενο γινόμενο είναι 
 έχει τις ίδιες ρίζες με το πολυώνυμο
έχει τις ίδιες ρίζες με το πολυώνυμο  και ο μεγιστοβάθμιος συντελεστής τους είναι ίσος με
και ο μεγιστοβάθμιος συντελεστής τους είναι ίσος με  . Άρα τα πολυώνυμα είναι ίσα. Οπότε έχουμε
. Άρα τα πολυώνυμα είναι ίσα. Οπότε έχουμε  . Από όπου εύκολα βλέπουμε ότι
. Από όπου εύκολα βλέπουμε ότι  .
.

 κ.ο.κ
κ.ο.κ![\displaystyle \Pi_{n} = 2^{n-1} \cdot \left ( \prod_{k=1}^{\left [ \dfrac{n}{2} \right ]} \sin \dfrac{k\pi}{n} \right )^{2} \displaystyle \Pi_{n} = 2^{n-1} \cdot \left ( \prod_{k=1}^{\left [ \dfrac{n}{2} \right ]} \sin \dfrac{k\pi}{n} \right )^{2}](/forum/ext/geomar/texintegr/latexrender/pictures/b34304dfbc01358d8d0683e00e1318dd.png)
 ) θα είναι
) θα είναι![\displaystyle T_{n} = \prod_{k=1}^{\left [ \dfrac{n}{2} \right ]} \sin \dfrac{k\pi}{n} = \sqrt{\dfrac{n}{2^{n-1}} \displaystyle T_{n} = \prod_{k=1}^{\left [ \dfrac{n}{2} \right ]} \sin \dfrac{k\pi}{n} = \sqrt{\dfrac{n}{2^{n-1}}](/forum/ext/geomar/texintegr/latexrender/pictures/bc3fd4f41b53abeefb0cdf43172608a4.png)
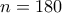 παίρνουμε το αποτέλεσμα της άσκησης που έθεσε αρχικά ο Ορέστης (παραπομπή).
παίρνουμε το αποτέλεσμα της άσκησης που έθεσε αρχικά ο Ορέστης (παραπομπή).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες