Σελίδα 1 από 1
Διπλάσια γωνία 40
Δημοσιεύτηκε: Πέμ Οκτ 18, 2018 1:32 pm
από KARKAR

- Διπλάσια γωνία.png (8.4 KiB) Προβλήθηκε 1071 φορές
Στο ορθογώνιο τρίγωνο του σχήματος , δείξτε ότι

. Λύσεις
με χρήση τριγωνομετρίας δεκτές , αν και όχι ιδιαίτερα επιθυμητές

Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Πέμ Οκτ 18, 2018 2:58 pm
από Γιώργος Μήτσιος
Καλό απόγευμα.

- Διπλάσια γωνία.PNG (7.72 KiB) Προβλήθηκε 1055 φορές
Το

είναι το συμμετρικό του

ως προς το

. Τότε

Με Π.Θ είναι

και

. Ισχύει
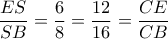
άρα από το αντίστροφο του Θ. διχοτόμου η
 διχοτόμος
διχοτόμος της

δηλ.

Φιλικά , Γιώργος.
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Πέμ Οκτ 18, 2018 4:30 pm
από george visvikis
Καλησπέρα!
Μία ανεπιθύμητη.

- Διπλάσια γωνία 40.png (10.2 KiB) Προβλήθηκε 1043 φορές
Θεωρώ σημείο

της

ώστε

και έστω

το μέσο της

Το τρίγωνο

είναι ισοσκελές, άρα

Με νόμο συνημιτόνων στο

βρίσκω
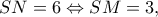
οπότε
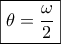
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Πέμ Οκτ 18, 2018 5:26 pm
από Altrian
Καλησπέρα σε όλους.
Αφού μας πρόλαβε ο Γιώργος Μήτσιος (γειά σου Γιώργο) μια ακόμα επιθυμητή που βασίζεται στο σχήμα του Γιώργου Βισβίκη.

(δύο πλευρές ανάλογες και την περιεχόμενη γωνία ίση (κοινή)) με λόγο ομοιότητας

Αρα

.
Αλέξανδρος Τριανταφυλλάκης
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Πέμ Οκτ 18, 2018 6:03 pm
από STOPJOHN
KARKAR έγραψε: ↑Πέμ Οκτ 18, 2018 1:32 pm
Διπλάσια γωνία.pngΣτο ορθογώνιο τρίγωνο του σχήματος , δείξτε ότι

. Λύσεις
με χρήση τριγωνομετρίας δεκτές , αν και όχι ιδιαίτερα επιθυμητές

Καλησπέρα
Aν είναι η

διχοτόμος της γωνίας

Εστω οτι
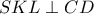
θα αποδείξω ότι

Απο το Πυθαγόρειο θεώρημα στο τρίγωνο

και

Το θεώρημα της διχοτόμου στο τρίγωνο

και Θ.Stweart στο τρίγωνο

Γιάννης
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Πέμ Οκτ 18, 2018 6:11 pm
από george visvikis
Και μία ακόμα επιθυμητή.

- Διπλάσια γωνία 40.β.png (8.04 KiB) Προβλήθηκε 1016 φορές
Φέρνω

και είναι:
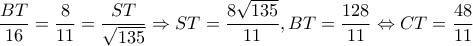
Αντικαθιστώντας αυτές τις τιμές στις πλευρές του τριγώνου

παρατηρώ ότι:


Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Πέμ Οκτ 18, 2018 6:45 pm
από nickchalkida
Αρκεί να αποδείξω ότι οι δοθέντες αριθμοί επαληθεύουν την κατασκευή της νεύσης.
Φέρω κάθετη στην

στο

και προεκτείνω την την

έως να τμήση την κάθετη στο

.
Υπολογίζω διαδοχικά

Δηλαδή

που σημαίνει

.
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Παρ Οκτ 19, 2018 2:14 am
από Γιώργος Μήτσιος
Χαιρετώ όλους! Θα έλεγα ότι ενδιαφέρον έχει να προβάλουμε και την -κατά τον θεματοθέτη- ..

..πλέον ανεπιθύμητη.
Εικάζω ότι αυτή που ακολουθεί , την έχει βεβαίως κατά νου ο αγαπητός
Θανάσης αλλά δεν θα ήθελε να την ..αντικρύσει στις πρώτες λύσεις !
Βρήκαμε

άρα

οπότε

ενώ και
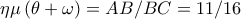
.
Προκύπτει

για
οξείες γωνίες , συνεπώς

.
Φιλικά , Γιώργος.
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Παρ Οκτ 19, 2018 7:03 am
από Μιχάλης Νάννος
KARKAR έγραψε: ↑Πέμ Οκτ 18, 2018 1:32 pm
Στο ορθογώνιο τρίγωνο του σχήματος , δείξτε ότι

. Λύσεις
με χρήση τριγωνομετρίας δεκτές , αν και όχι ιδιαίτερα επιθυμητές

Καλημέρα. Παραλλαγή της 1ης λύσης του φίλου Γιώργου Μήτσιου με πιο ‘δύσκολα’ νούμερα.

- shape.png (15.43 KiB) Προβλήθηκε 971 φορές
Φέρνω τη διχοτόμο

της

και παρατηρώ πως η

είναι διχοτόμος της

Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Παρ Οκτ 19, 2018 12:49 pm
από Doloros
Γράφω, προς το μέρος του

, το ημικύκλιο κέντρου

και διαμέτρου

.
Φέρνω από το

την ακτίνα

. Ας είναι

τα σημεία τομής της
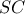
με το ημικύκλιο και την ευθεία

.
Είναι απλό να δούμε ότι:

- Διπλάσια γωνία 40.png (46.24 KiB) Προβλήθηκε 946 φορές
1.

και
2.

και έτσι
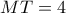
Τα ορθογώνια τρίγωνα

έχουν τις οξείες γωνίες στα

ισες και τις πλευρές αυτών ανάλογες άρα είναι όμοια συνεπώς

που εξασφαλίζει το ζητούμενο .
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Παρ Οκτ 19, 2018 9:11 pm
από Μιχάλης Τσουρακάκης
KARKAR έγραψε: ↑Πέμ Οκτ 18, 2018 1:32 pm
Διπλάσια γωνία.pngΣτο ορθογώνιο τρίγωνο του σχήματος , δείξτε ότι

. Λύσεις
με χρήση τριγωνομετρίας δεκτές , αν και όχι ιδιαίτερα επιθυμητές

Είναι,

οπότε

κι έστω ότι η μεσοκάθετος της

τέμνει την

στο

και την

στο

Τότε,

Για τον κύκλο

ισχύει

αφού
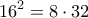
Άρα

εφαπτόμενη του

,επομένως


- διπλάσια γωνία.png (62.69 KiB) Προβλήθηκε 912 φορές
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Σάβ Οκτ 20, 2018 8:15 am
από Μιχάλης Νάννος
Έστω

και

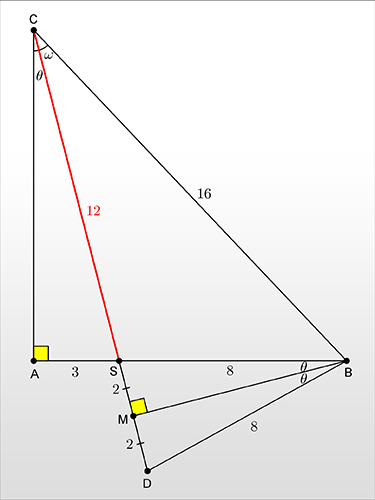
- shape2.png (12.61 KiB) Προβλήθηκε 892 φορές
Από

και από

Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Κυρ Οκτ 21, 2018 2:53 pm
από Γιώργος Μήτσιος
Χαιρετώ και πάλι!

- 21-10 Διπλάσια γωνία.PNG (6.18 KiB) Προβλήθηκε 856 φορές
Στο τρίγωνο

για τις πλευρές ισχύει

άρα με την πρόταση

(αποδείξεις στο θέμα
Πέντε παρά ..κάτι )παίρνουμε

αλλά έχουμε και

οπότε

..
Ας μου επιτραπεί να χαρίσω αυτή τη λύση στον αγαπητό
Γιώργο Ρίζο , εφόσον τέρπεται με λύσεις
χωρίς βοηθητικές
αλλά και διότι (με το δίκιο του να ) ..εγείρεται άμα η (προσφιλής μας)
Τριγωνομετρία τίθεται υπό..

.."περιορισμένη ευαρέσκεια''
Φιλικά (πάντοτε και προς όλους) , Γιώργος.
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Κυρ Οκτ 21, 2018 7:25 pm
από Γιώργος Ρίζος
Στον φίλο
Γιώργο Μήτσιο ως αντίδωρο, για την αφιέρωση και για τις όμορφες γεωμετρικές εμπνεύσεις που μοιράζεται μαζί μας.
Δίχως βοηθητικές, με ολίγη ... τριγωνομετρία.

- 21-10 Διπλάσια γωνία.PNG (6.18 KiB) Προβλήθηκε 837 φορές
Από Πυθαγόρειο Θεώρημα στο

είναι

και στο
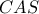
είναι

.
Από Τριγωνομετρικό CEVA στο

είναι

.
Είναι

.
Άρα

και αφού οι γωνίες είναι οξείες, θα είναι
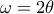
.
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Κυρ Οκτ 21, 2018 7:44 pm
από KARKAR
Γιώργος Μήτσιος έγραψε: ↑Κυρ Οκτ 21, 2018 2:53 pm
.. η (προσφιλής μας)
Τριγωνομετρία τίθεται υπό..

.."περιορισμένη ευαρέσκεια''
Φιλικά (πάντοτε και προς όλους) , Γιώργος .
Μία προσφιλής έκφραση του KARKAR ( σχεδόν moto , για τους γνωρίζοντες ) , είναι :
"Λίγη τριγωνομετρία δεν έβλαψε ποτέ κανέναν " . Αλλά εδώ πρόκειται για πόκα :
Πότε κερδίζει η κέντα , πότε τα τρία , στην περίπτωσή μας η κέντα ( ευκλείδεια λύση

)
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Κυρ Οκτ 21, 2018 11:54 pm
από Γιώργος Μήτσιος
Καλό βράδυ. Ασφαλώς και είναι γνωστή η ως άνω έκφραση του φίλου
KARKAR. Ο ίδιος την στήριξε δίνοντας ουκ ολίγες φορές και τριγωνομετρικές λύσεις !
Στη συνέχεια μια ακόμη προσέγγιση υπέρ της ..
κέντας !

- 21-10 Διπλάσια γωνία ΚΑRKAR.PNG (6.95 KiB) Προβλήθηκε 816 φορές
Με το

μέσον της

και

την τομή των
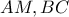
έχουμε

και

. Αρκεί να δείξουμε ότι
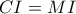
.
Ας επικαλεστούμε δις τον
Μενέλαο : Στο τρίγωνο

με διατέμνουσα την

παίρνουμε

και στο

με διατέμνουσα την

προκύπτει

άρα

.
Φιλικά , Γιώργος.
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Τρί Οκτ 23, 2018 11:20 am
από Doloros
Στο τρίγωνο

φέρνω τη διχοτόμο

και στο τρίγωνο

τη διάμεσο

.

( Π. Θ στα
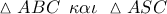
) .

( Θ . διχοτόμου στο

).

- Διπλάσια γωνία 40_new_1.png (35.57 KiB) Προβλήθηκε 772 φορές
Φέρνω τώρα τη κάθετη στην

στο

που τέμνει την ευθεία

στο

και τη κάθετη ,

, στο

από το

.
Επειδή προφανώς

τα ορθογώνια τρίγωνα

είναι όμοια .
Αλλά στο ισοσκελές τρίγωνο

το ύψος

είναι και διχοτόμος , άρα

.
Η άσκηση έγινε πολύ δημοφιλής και αυτό είναι πολύ ευχάριστο! . Τα μήκη  και
και  υπολογίζονται και είναι :
υπολογίζονται και είναι :  και
και  αντίστοιχα.
αντίστοιχα.
Re: Διπλάσια γωνία 40
Δημοσιεύτηκε: Τρί Οκτ 23, 2018 1:08 pm
από STOPJOHN
KARKAR έγραψε: ↑Πέμ Οκτ 18, 2018 1:32 pm
Διπλάσια γωνία.pngΣτο ορθογώνιο τρίγωνο του σχήματος , δείξτε ότι

. Λύσεις
με χρήση τριγωνομετρίας δεκτές , αν και όχι ιδιαίτερα επιθυμητές

Καλημέρα μια λύση ακόμη με το Θ.Θαλή που θα τρίζουν τα κόκκαλα του με τον εξοβελισμό της Γεωμετρίας ....
Εστω ότι

Ειναι

Απο το Πυθαγόρειο Θεώρημα .Εφόσον

Τα τρίγωνα
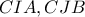
είναι όμοια γιατί είναι ορθογώνια και

συνεπώς

Γιάννης
 . Λύσεις
. Λύσεις 
 . Λύσεις
. Λύσεις  είναι το συμμετρικό του
είναι το συμμετρικό του  ως προς το
ως προς το  . Τότε
. Τότε 
 και
και  . Ισχύει
. Ισχύει 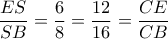
 διχοτόμος της
διχοτόμος της  δηλ.
δηλ. 
 της
της  ώστε
ώστε  και έστω
και έστω  το μέσο της
το μέσο της  Το τρίγωνο
Το τρίγωνο  είναι ισοσκελές, άρα
είναι ισοσκελές, άρα 
 βρίσκω
βρίσκω 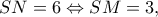 οπότε
οπότε 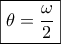
 (δύο πλευρές ανάλογες και την περιεχόμενη γωνία ίση (κοινή)) με λόγο ομοιότητας
(δύο πλευρές ανάλογες και την περιεχόμενη γωνία ίση (κοινή)) με λόγο ομοιότητας 
 .
. διχοτόμος της γωνίας
διχοτόμος της γωνίας 
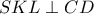 θα αποδείξω ότι
θα αποδείξω ότι 
 και
και 


 και είναι:
και είναι: 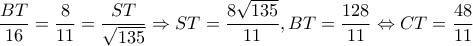
 παρατηρώ ότι:
παρατηρώ ότι: 

 στο
στο  και προεκτείνω την την
και προεκτείνω την την  .
.
 που σημαίνει
που σημαίνει  .
. άρα
άρα  οπότε
οπότε 
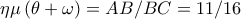 .
. για οξείες γωνίες , συνεπώς
για οξείες γωνίες , συνεπώς  .
. και παρατηρώ πως η
και παρατηρώ πως η 
 και διαμέτρου
και διαμέτρου  .
. . Ας είναι
. Ας είναι  τα σημεία τομής της
τα σημεία τομής της 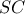 με το ημικύκλιο και την ευθεία
με το ημικύκλιο και την ευθεία  .
. και
και  και έτσι
και έτσι 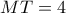
 έχουν τις οξείες γωνίες στα
έχουν τις οξείες γωνίες στα  ισες και τις πλευρές αυτών ανάλογες άρα είναι όμοια συνεπώς
ισες και τις πλευρές αυτών ανάλογες άρα είναι όμοια συνεπώς  που εξασφαλίζει το ζητούμενο .
που εξασφαλίζει το ζητούμενο . οπότε
οπότε  κι έστω ότι η μεσοκάθετος της
κι έστω ότι η μεσοκάθετος της  τέμνει την
τέμνει την  στο
στο  και την
και την  στο
στο 

 ισχύει
ισχύει  αφού
αφού 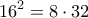

 και
και 
 και από
και από 
 για τις πλευρές ισχύει
για τις πλευρές ισχύει  άρα με την πρόταση
άρα με την πρόταση 
 αλλά έχουμε και
αλλά έχουμε και  οπότε
οπότε  ..
.. είναι
είναι  και στο
και στο 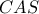 είναι
είναι  .
. .
. και αφού οι γωνίες είναι οξείες, θα είναι
και αφού οι γωνίες είναι οξείες, θα είναι 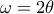 .
. την τομή των
την τομή των 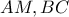 έχουμε
έχουμε  και
και  . Αρκεί να δείξουμε ότι
. Αρκεί να δείξουμε ότι 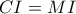 .
. παίρνουμε
παίρνουμε 
 με διατέμνουσα την
με διατέμνουσα την  προκύπτει
προκύπτει  άρα
άρα  φέρνω τη διχοτόμο
φέρνω τη διχοτόμο  και στο τρίγωνο
και στο τρίγωνο  τη διάμεσο
τη διάμεσο  .
. ( Π. Θ στα
( Π. Θ στα 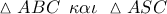 ) .
) .  ( Θ . διχοτόμου στο
( Θ . διχοτόμου στο  και τη κάθετη ,
και τη κάθετη , , στο
, στο  .
. τα ορθογώνια τρίγωνα
τα ορθογώνια τρίγωνα  είναι όμοια .
είναι όμοια .  το ύψος
το ύψος  .
. και
και  και
και  αντίστοιχα.
αντίστοιχα.