Γράφω την λύση του Dodgson, που μου άρεσε.
Την κάνω σε δύο βήματα (όπως ο ίδιος) για λόγους διδακτικούς, αν και δεν είναι απαραίτητα και τα δύο αλλά μπορούμε να πάμε απευθείας στο δεύτερο τμήμα της λύσης του. Επίσης θα είμαι λίγο αναλυτικός επειδή μας διαβάζουν μαθητές.
Έστω για ευκολία ότι ο ένας αριθμός είναι ο

(η γενίκευση, μετά). Γράφουμε τον

, όπου

, στο δεκαδικό του ανάπτυγμα, οπότε υπάρχει ένα αρχικό κομμάτι

μήκους

(μπορεί να είναι
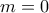
) και ένα περιοδικό κομμάτι

μήκους

τέτοια ώστε
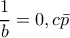
. Προσοχή, το ανάπτυγμα είναι σίγουρα άπειρο περιοδικό - δεν τελειώνει - ακριβώς γιατί ο

δεν περιέχει

ή

ως πρώτο παράγοντα.
Προσθέτουμε τώρα το περιοδικό κομμάτι ως γεωμετρική πρόοδο με λόγο

. Θα βρούμε

και άρα, διώχνοντας τους παρονομαστές, θα βρούμε

Όμως το

διαιρεί το δεξί μέλος και επειδή είναι πρώτο προς το

, και άρα προς το

, έπεται ότι

. Τελειώσαμε! Αυτό είναι το αποδεικτέο.
Γενικά τώρα. Κάνουμε ακριβώς την ίδια δουλειά αλλά αντί να γράψουμε το

στο δεκαδικό του ανάπτυγμα, το γράφουμε ως προς βάση το

. Ρουά ματ.
 πρώτοι προς αλλήλους φυσικοί αριθμοί, να αποδειχθεί ότι υπάρχει φυσικός αριθμός
πρώτοι προς αλλήλους φυσικοί αριθμοί, να αποδειχθεί ότι υπάρχει φυσικός αριθμός  τέτοιος ώστε ο
τέτοιος ώστε ο  να διαιρεί τον
να διαιρεί τον  .
.
 για κάθε
για κάθε  .
.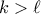 φυσικοί, ώστε
φυσικοί, ώστε  και
και  .
. , άρα
, άρα  , και αφού
, και αφού  , έχω
, έχω 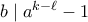 , άτοπο από την αρχική μας υπόθεση ότι
, άτοπο από την αρχική μας υπόθεση ότι  ό.έ.δ.
ό.έ.δ. η ανάλυση του
η ανάλυση του  , όπου
, όπου  η συνάρτηση του Euler και έχουμε το ζητούμενο καθώς
η συνάρτηση του Euler και έχουμε το ζητούμενο καθώς  κι έτσι
κι έτσι  . Όμοια
. Όμοια 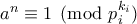 για κάθε
για κάθε  κι έτσι
κι έτσι  .
. . (Όπως είπε και ο Σταύρος πιο πάνω.) Μάλλον όμως κάτι άλλο έχει υπόψη του ο Μιχάλης.
. (Όπως είπε και ο Σταύρος πιο πάνω.) Μάλλον όμως κάτι άλλο έχει υπόψη του ο Μιχάλης. (η γενίκευση, μετά). Γράφουμε τον
(η γενίκευση, μετά). Γράφουμε τον  , όπου
, όπου  , στο δεκαδικό του ανάπτυγμα, οπότε υπάρχει ένα αρχικό κομμάτι
, στο δεκαδικό του ανάπτυγμα, οπότε υπάρχει ένα αρχικό κομμάτι  μήκους
μήκους  (μπορεί να είναι
(μπορεί να είναι  ) και ένα περιοδικό κομμάτι
) και ένα περιοδικό κομμάτι  μήκους
μήκους  . Προσοχή, το ανάπτυγμα είναι σίγουρα άπειρο περιοδικό - δεν τελειώνει - ακριβώς γιατί ο
. Προσοχή, το ανάπτυγμα είναι σίγουρα άπειρο περιοδικό - δεν τελειώνει - ακριβώς γιατί ο  ή
ή  ως πρώτο παράγοντα.
ως πρώτο παράγοντα.  . Θα βρούμε
. Θα βρούμε 

 , και άρα προς το
, και άρα προς το  , έπεται ότι
, έπεται ότι  . Τελειώσαμε! Αυτό είναι το αποδεικτέο.
. Τελειώσαμε! Αυτό είναι το αποδεικτέο. . Ρουά ματ.
. Ρουά ματ.