 , ισχύει ότι :
, ισχύει ότι :  , με
, με  σταθερό .
σταθερό .α) Υπολογίστε την ελάχιστη τιμή της παράστασης :

β) Να συγκριθούν οι ελάχιστες τιμές της
 , για
, για 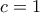 και
και  .
.γ) Για ποια τιμή του
 , η ελάχιστη τιμή της
, η ελάχιστη τιμή της  , είναι η μικρότερη δυνατή ;
, είναι η μικρότερη δυνατή ; , ισχύει ότι :
, ισχύει ότι :  , με
, με  σταθερό .
σταθερό .
 , για
, για 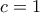 και
και  .
. , η ελάχιστη τιμή της
, η ελάχιστη τιμή της  , είναι η μικρότερη δυνατή ;
, είναι η μικρότερη δυνατή ; με
με  από γνωστή πρόταση.
από γνωστή πρόταση. 


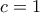 , έχουμε
, έχουμε  για
για  παίρνουμε
παίρνουμε 
 από την
από την  με την αντικατάσταση
με την αντικατάσταση  Η παράγωγος της είναι
Η παράγωγος της είναι  που μας οδηγεί στην ελάχιστη τιμή της
που μας οδηγεί στην ελάχιστη τιμή της  που είναι η
που είναι η  Επειδή όμως θέλουμε το ελάχιστο της
Επειδή όμως θέλουμε το ελάχιστο της  , εύκολα προκύπτει
, εύκολα προκύπτει  για
για 
α) Είναι
 , άρα
, άρα  και επίσης
και επίσης  . Οπότε
. Οπότε 

 . Άρα το δεξί μέλος είναι το ζητούμενο ελάχιστο.
. Άρα το δεξί μέλος είναι το ζητούμενο ελάχιστο. 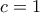 και
και  η προηγούμενη παράσταση ελαχίστου παίρνει την ίδια τιμή,
η προηγούμενη παράσταση ελαχίστου παίρνει την ίδια τιμή,  .
. με ισότητα αν
με ισότητα αν  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες