Ανισοτική σε τρίγωνο

#1

είναι τα ύψη οξυγώνιου τριγώνου ABC.

Να δείξετε ότι $DE+DF\le BC.$ Πότε ισχύει η ισότητα;

ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ · #2

george visvikis έγραψε: ↑
Παρ Μάιος 08, 2020 6:59 pm
είναι τα ύψη οξυγώνιου τριγώνου Να δείξετε ότι $DE+DF\le BC.$ Πότε ισχύει η ισότητα;

Καλησπέρα!

Είναι $\rm BDF,DCE$ όμοια άρα $\rm \dfrac{DF}{AC}=\dfrac{BF}{BC}\Leftrightarrow FD=\dfrac{BF\cdot AC}{BC}=b\cos \angle B$ .Ομοίως $\rm DE=c\cos \angle C$ .
Είναι γνωστό ότι $\rm b\cos\angle B+c\cos \angle C+a\cos \angle A=2a\sin \angle B\sin \angle C\Leftrightarrow DF+DE=2a\sin \angle B\sin \angle C-a\cos \angle A$
Αρκεί λοιπόν $\rm 2a\sin \angle B\sin \angle C-a\cos \angle A\leq a\Leftrightarrow 2\sin \angle B\sin \angle C\leq \cos \angle A+1\Leftrightarrow$
$\rm \cos(\angle B-\angle C)-\cos(\angle B+\angle C)\leq\cos\angle A+1\Leftrightarrow\cos(\angle B-\angle C)\leq 1$ που ισχύει.
Η ισότητα όταν $\rm \cos(\angle B-\angle C)=1=\cos0$ δηλαδή όταν $\rm AB=AC$ .

Al.Koutsouridis · #3

Μια άλλη λύση είναι να παρατηρήσουμε ότι τα σημεία F,E,D

και το μέσο της πλευράς

, έστω

, είναι ομοκυκλικά (κύκλος Euler). Το σημείο

είναι το μέσο του τόξου FDME

, άρα $MF+ME \geq DF+DE$ . Από την ομοκυκλικότητα των B,F,E,C

σε κύκλο με διάμετρο την πλευρά

είναι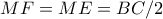

, που δίνει το ζητούμενο. Η ισότητα ισχύει όταν το

ταυτιστεί με το μέσο της πλευράς

, δηλαδή όταν το τρίγωνο είναι ισοσκελές.

S.E.Louridas · #4

Αν θεωρήσουμε

το συμμετρικό του

ως προς

, τότε, τα σημεία E,F,B,L,C,

είναι ομοκυκλικά και ανήκουν σε κύκλο διαμέτρου BC.

Όμως τα

είναι κατά τα γνωστά συνευθειακά (αποδεικνύεται εξάλλου εύκολα και άμεσα, δηλ. $\angle BDL = \angle FDB = \angle A = \angle CDE$ ),
με τη χορδή

πλέον να είναι μικρότερη ή ίση της διαμέτρου

.
Δηλαδή ισχύει $LE \leqslant BC \Rightarrow LD + DE \leqslant BC \Rightarrow DF + DE \leqslant BC.$
Προφανώς η ισότητα ισχύει όταν το τρίγωνο ABC

είναι ισοσκελές.

: ασζχ.png (21.44 KiB) Προβλήθηκε 751 φορές

Ανισοτική σε τρίγωνο

Ανισοτική σε τρίγωνο

Re: Ανισοτική σε τρίγωνο

Re: Ανισοτική σε τρίγωνο

Re: Ανισοτική σε τρίγωνο

Μέλη σε σύνδεση