Παραβολή και εμβαδόν

#1

: Παραβολή και εμβαδόν.png (17.11 KiB) Προβλήθηκε 728 φορές

Δίνεται η παραβολή $\displaystyle C:y = k{x^2},k > 0$ και τα σημεία της $\displaystyle A(a,k{a^2}),B(b,k{b^2}),a < 0 < b.$

Οι εφαπτόμενες της παραβολής στα A, B

τέμνονται στο

και η κάθετη από το

στον

τέμνει την

παραβολή στο

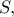τη χορδή

στο

και έστω

ένα οποιοδήποτε σημείο του τόξου $\overset\frown{AOB}.$

α) Να δείξετε ότι

είναι το μέσο του τμήματος AB.

β) Να υπολογίσετε το (SAB)

συναρτήσει των a, b,k

και να δείξετε ότι $\displaystyle (NAB) \le (SAB).$

#2

Δεν γράφω λύση για να ασχοληθούν όσοι δεν την γνωρίζουν ήδη, αλλά είναι πειρασμός να κάνω ένα ιστορικό σχόλιο:

Τα παραπάνω σε μικρή παραλλαγή υπάρχουν στο Τετραγωνισμός ορθογωνίου κώνου τομής του μέγα Αρχιμήδη, Προτάσεις

και

. Εκεί δείχνει ακόμη ότι το εμβαδόν του παραβολικού χωρίου AOSB

είναι τα $\frac {4}{3}$ του τριγώνου ASB

, και αυτά χωρίς χρήση ολοκλήρωσης. Τα Μαθηματικά στον συλλογισμό του είναι ανεξίτηλα κομμάτια από την ιστορία των Μαθηματικών. Δείγματα της μεγαλοφυΐας του.

ΦΩΤΙΑΔΗΣ ΠΡΟΔΡΟΜΟΣ · #3

: 325.PNG (30.32 KiB) Προβλήθηκε 673 φορές

α)
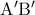Έστω $\rm A',B'$ οι προβολές των $\rm A,B$ στην διευθετούσα της παραβολής ,η οποία είναι παράλληλη στον $\rm xx'$ .Είναι $\rm PA'=PF=PB'$ όπου $\rm F$ η εστία της παραβολής,οπότε $\rm PS$ μεσοκάθετος του $\rm A'B'$ και από το τραπέζιο $\rm A'B'BA$ έπεται το ζητούμενο.
β) Επειδή η $\rm PM$ είναι μεσοπαράλληλη των $\rm AA',BB'$ η τετμημένη του $\rm S$ είναι $\rm \dfrac{a+b}{2}$ και έτσι η τεταγμένη του $\rm k\dfrac{(a+b)^2}{4}$ .Θα δείξω πρώτα ότι $\rm (SAB)>(NAB),S\not \equiv N$ ,με $\rm N$ στο $\rm AOB$ .
Εύκολα προκύπτει ότι η $\rm AB$ έχε εξίσωση $\rm y+x(-ka-kb)+akb=0$ .Αρκεί $\rm d(S,AB)>d(N,AB)$ το οποίο από τον γνωστό τύπο για την απόσταση σημείου από ευθείας οδηγεί στο (απλοποιώ τους κοινούς παρονομαστές) $\rm \left | y_N+x_N(-ka-kb+akb) \right |< \rm \left | y_S+x_S(-ka-kb+akb) \right |$
Είναι $\rm \left | y_N+x_N(-ka-kb+akb) \right |=k\left | x_N^2-(a+b)x_N+ab \right |=k\left | (x_N-a)\left ( x_N-b \right ) \right |=k\left ( a-x_N \right )\left ( x_N-b \right )$ (το τελευταίο επειδή $\rm a<x_N<b$ .
Το τριώνυμο $\rm -x_N^2+x_N(a+b)-ab$ εμφανίζει μέγιστο για $\rm x_N=\dfrac{a+b}{2}=x_S$ .Το ζητούμενο έπεται.
Για το $\rm (ASB)$ αντικαθιστούμε στον τύπο για την απόσταση από την $\rm AB$ τις συντετεγμένες του $\rm S$ και έχουμε:
$\rm (ASB)=\dfrac{1}{2}d\left ( S,AB \right )\cdot AB=\dfrac{1}{2}\dfrac{\left | k\dfrac{(a+b)^2}{4}-k\dfrac{\left ( a+b \right )^2}{2}+abk \right |}{\sqrt{1+k^2(a+b)^2}}\sqrt{(b-a)^2+(b-a)^2(b+a)^2k^2}=$
$\rm =\dfrac{1}{8}(b-a)k\left |-a^2-b^2+2ab \right |=\frac{k}{8}(b-a)^3$

Παρατήρηση: Μπορούμε επίσης να δείξουμε (χωρίς αναλυτική) ότι $\rm (APB)=2(ASB)$

KARKAR · #4

: Παραβολή και εμβαδόν.png (21.39 KiB) Προβλήθηκε 660 φορές

Με χρήση ανάλυσης : Το σημείο

, ( όπως και το

) , έχει τετμημένη : $\dfrac{a+b}{2}$

( εφαρμογή του σχολικού στο Θ.Μ.Τ.)

Η κυρτότητα της παραβολής φέρνει το

στο εσωτερικό της ζώνης των παραλλήλων ...

Παραβολή και εμβαδόν

Παραβολή και εμβαδόν

Re: Παραβολή και εμβαδόν

Re: Παραβολή και εμβαδόν

Re: Παραβολή και εμβαδόν

Μέλη σε σύνδεση