Αν
 είναι το τρίγωνο με κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου τριγώνου
είναι το τρίγωνο με κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου τριγώνου  και
και  είναι το ορθικό τρίγωνο του τριγώνου
είναι το ορθικό τρίγωνο του τριγώνου  τότε
τότε
 είναι το τρίγωνο με κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου τριγώνου
είναι το τρίγωνο με κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου τριγώνου  και
και  είναι το ορθικό τρίγωνο του τριγώνου
είναι το ορθικό τρίγωνο του τριγώνου  τότε
τότε
ΈστωΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Παρ Απρ 16, 2021 2:59 pmΞεφύλλιζα το βιβλίο '' ΘΕΩΡΗΜΑΤΑ ΚΑΙ ΠΡΟΒΛΗΜΑΤΑ ΓΕΩΜΕΤΡΙΑΣ '' του Νίκου Κισκύρα και πιο συγκεκριμένα το ''Επιπεδομετρία Βιβλίο Τέταρτον-Βιβλίο Πέμπτον''. Μέσα στον πλούτο των άλυτων θεμάτων, το μάτι μου έπεσε στην πρόταση 1550β στη σελίδα 400. Κάτι θυμήθηκα όταν την είδα...
Ανείναι το τρίγωνο με κορυφές τα σημεία επαφής του εγγεγραμμένου κύκλου τριγώνου
και
είναι το ορθικό τρίγωνο του τριγώνου
τότε

 οι ακτίνες του περιγεγραμμένου και του εγγεγραμμένου κύκλου του
οι ακτίνες του περιγεγραμμένου και του εγγεγραμμένου κύκλου του  αντίστοιχα και
αντίστοιχα και 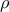 η ακτίνα του
η ακτίνα του  που είναι ο κύκλος του
που είναι ο κύκλος του 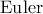 του τριγώνου
του τριγώνου  Δηλαδή
Δηλαδή 

 είναι όμοια
είναι όμοια  , άρα
, άρα  και το ζητούμενο αποδείχτηκε.
και το ζητούμενο αποδείχτηκε. Τα τρίγωνα
Τα τρίγωνα  έχουν τις πλευρές τους παράλληλες. Αν μου ζητηθεί θα το αποδείξω.
έχουν τις πλευρές τους παράλληλες. Αν μου ζητηθεί θα το αποδείξω.Το έχεις ήδη κάνει Γιώργο στην παρακάτω δημοσίευσηgeorge visvikis έγραψε: ↑Παρ Απρ 16, 2021 5:43 pmΤα τρίγωνα
έχουν τις πλευρές τους παράλληλες. Αν μου ζητηθεί θα το αποδείξω.
ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Παρ Απρ 16, 2021 7:43 pmΤο έχεις ήδη κάνει Γιώργο στην παρακάτω δημοσίευσηgeorge visvikis έγραψε: ↑Παρ Απρ 16, 2021 5:43 pmΤα τρίγωνα
έχουν τις πλευρές τους παράλληλες. Αν μου ζητηθεί θα το αποδείξω.
viewtopic.php?f=22&t=64236
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες