 . Εξάλλου, η πρόοδος έχει τουλάχιστον τρεις όρους. Ποιός είναι ο μεγαλύτερος αριθμός που μπορεί να αποτελεί όρο μιας τέτοιας προόδου;
. Εξάλλου, η πρόοδος έχει τουλάχιστον τρεις όρους. Ποιός είναι ο μεγαλύτερος αριθμός που μπορεί να αποτελεί όρο μιας τέτοιας προόδου;Για Β' & Γ' Λυκείου. Πηγή: Ενιαία Κρατική Εξέταση Ρωσία, 2021.
 . Εξάλλου, η πρόοδος έχει τουλάχιστον τρεις όρους. Ποιός είναι ο μεγαλύτερος αριθμός που μπορεί να αποτελεί όρο μιας τέτοιας προόδου;
. Εξάλλου, η πρόοδος έχει τουλάχιστον τρεις όρους. Ποιός είναι ο μεγαλύτερος αριθμός που μπορεί να αποτελεί όρο μιας τέτοιας προόδου;Απάντηση:Al.Koutsouridis έγραψε: ↑Σάβ Σεπ 11, 2021 11:57 amΟ πρώτος όρος (πεπερασμένου αριθμού όρων) γεωμετρικής προόδου, που αποτελείται από τριψήφιους φυσικούς αριθμούς, είναι ίσος με. Εξάλλου, η πρόοδος έχει τουλάχιστον τρεις όρους. Ποιός είναι ο μεγαλύτερος αριθμός που μπορεί να αποτελεί όρο μιας τέτοιας προόδου;
 μέσω της
μέσω της 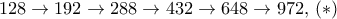 (ο λόγος είναι
(ο λόγος είναι  ).
). αλλά γλιτώνουμε την περιπτωσιολογία.
αλλά γλιτώνουμε την περιπτωσιολογία. , όπου
, όπου  πρώτοι προς αλλήλους με
πρώτοι προς αλλήλους με  . Τότε ο δεύτερος όρος είναι
. Τότε ο δεύτερος όρος είναι  , άρα
, άρα 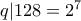 . Είναι λοιπόν
. Είναι λοιπόν  για κάποιον
για κάποιον  από
από  έως
έως  .
. ο λόγος είναι
ο λόγος είναι  (φυσικός). Μία πιθανή γεωμετρική πρόοδος είναι (παίρνω
(φυσικός). Μία πιθανή γεωμετρική πρόοδος είναι (παίρνω  ) η
) η  . Για
. Για  δεν υπάρχει πρόοδος με τρεις τριψήφιους όρους (ήδη ο τρίτος ξεπερνά το
δεν υπάρχει πρόοδος με τρεις τριψήφιους όρους (ήδη ο τρίτος ξεπερνά το  ). Το κρατάμε και ελέγχουμε τις άλλες περιπτώσεις.
). Το κρατάμε και ελέγχουμε τις άλλες περιπτώσεις. . Τότε η περίπτωση
. Τότε η περίπτωση  δίνει την
δίνει την  . Η
. Η  δίνει
δίνει  και εδώ σταματάει. Για
και εδώ σταματάει. Για 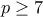 δεν υπάρχει πρόοδος με τρεις τριψήφιους όρους (ήδη ο τρίτος ξεπερνά το
δεν υπάρχει πρόοδος με τρεις τριψήφιους όρους (ήδη ο τρίτος ξεπερνά το  ).
). . Για
. Για  παίρνουμε
παίρνουμε  . Εδώ σταματάει γιατί ο επόμενος όρος δεν είναι ακέραιος. Για
. Εδώ σταματάει γιατί ο επόμενος όρος δεν είναι ακέραιος. Για  παίρνουμε
παίρνουμε  . Εδώ σταματάει. Για
. Εδώ σταματάει. Για  δίνει
δίνει  . Για
. Για  δίνει
δίνει 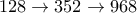 (που είναι κοντά στην απάντηση, γι' αυτό και δεν μπορούμε να αποφύγουμε την περιπτωσιολογία). Τα μεγαλύτερα
(που είναι κοντά στην απάντηση, γι' αυτό και δεν μπορούμε να αποφύγουμε την περιπτωσιολογία). Τα μεγαλύτερα  αποκλείονται γιατί δεν δίνουν τρεις όρους.
αποκλείονται γιατί δεν δίνουν τρεις όρους. . Για
. Για  παίρνουμε
παίρνουμε  και μετά είναι κλάσμα. Για
και μετά είναι κλάσμα. Για  παίρνουμε
παίρνουμε  . Για
. Για  παίρνουμε
παίρνουμε  . Όμοια οι περιπτώσεις
. Όμοια οι περιπτώσεις  (δεν τις γράφω για οικονομία αλλά μπορεί να ελέγξει κανείς). Τα πιο μεγάλα
(δεν τις γράφω για οικονομία αλλά μπορεί να ελέγξει κανείς). Τα πιο μεγάλα  δίνουν μόνο δύο όρους.
δίνουν μόνο δύο όρους. ή
ή  ή
ή  ή
ή  δεν χρειάζεται να τα δούμε γιατί ο τρίτος όρος έχει στον παρανομαστή όρο τουλάχιστον
δεν χρειάζεται να τα δούμε γιατί ο τρίτος όρος έχει στον παρανομαστή όρο τουλάχιστον  , και άρα δεν είναι ακέραιος.
, και άρα δεν είναι ακέραιος.  (στη λύση του Μιχάλη) είναι δύναμη του
(στη λύση του Μιχάλη) είναι δύναμη του  , τότε και ο αριθμός μας είναι δύναμη του
, τότε και ο αριθμός μας είναι δύναμη του  άρα το μέγιστο θα ήταν
άρα το μέγιστο θα ήταν  .
. περιττός πρώτος ο οποίος διαιρεί τον
περιττός πρώτος ο οποίος διαιρεί τον  . Τότε ο τελικός αριθμός είναι πολλαπλάσιος του
. Τότε ο τελικός αριθμός είναι πολλαπλάσιος του  .
. , τότε ο τελικός αριθμός είναι πολλαπλάσιος του
, τότε ο τελικός αριθμός είναι πολλαπλάσιος του 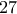 και για να είναι μεγαλύτερος του
και για να είναι μεγαλύτερος του  πρέπει να είναι ίσος με
πρέπει να είναι ίσος με  . Αυτό είναι άτοπο διότι
. Αυτό είναι άτοπο διότι  αλλά
αλλά  .
. , τότε ο τελικός αριθμός είναι πολλαπλάσιος του
, τότε ο τελικός αριθμός είναι πολλαπλάσιος του  και ο μεγαλύτερος τέτοιος τριψήφιος είναι ο
και ο μεγαλύτερος τέτοιος τριψήφιος είναι ο  .
. , τότε ο τελικός αριθμός είναι πολλαπλάσιος του
, τότε ο τελικός αριθμός είναι πολλαπλάσιος του  και ο μεγαλύτερος τέτοιος τριψήφιος είναι ο
και ο μεγαλύτερος τέτοιος τριψήφιος είναι ο  .
. τότε δεν υπάρχει τέτοιος τριψήφιος.
τότε δεν υπάρχει τέτοιος τριψήφιος.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες