Δίνεται ο δειγματικός χώρος
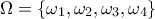 και τα ενδεχόμενα
και τα ενδεχόμενα 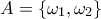 και
και  . Για τις πιθανότητες των απλών ενδεχομένων του
. Για τις πιθανότητες των απλών ενδεχομένων του  ισχύουν:
ισχύουν:

A. Να δείξετε ότι
 ,
,  ,
,  και
και  .
.Β. Να εξετάσετε αν τα ενδεχόμενα
 και
και  είναι ασυμβίβαστα.
είναι ασυμβίβαστα.Γ. Να βρείτε τις πιθανότητες των ενδεχομένων:
 "Το ενδεχόμενο να πραγματοποιούνται και τα δύο ενδεχόμενα
"Το ενδεχόμενο να πραγματοποιούνται και τα δύο ενδεχόμενα  ή κανένα".
ή κανένα".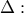 "Το ενδεχόμενο να μην πραγματοποιούνται ταυτόχρονα τα
"Το ενδεχόμενο να μην πραγματοποιούνται ταυτόχρονα τα  ".
".Δ. Αν
 , με
, με  , είναι σημεία της ευθείας
, είναι σημεία της ευθείας  , όπου
, όπου  πραγματική σταθερά, τότε να δείξετε ότι ισχύει η σχέση:
πραγματική σταθερά, τότε να δείξετε ότι ισχύει η σχέση: , όπου
, όπου 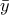 και
και  η μέση τιμή και η διάμεσος, αντίστοιχα, των τεταγμένων των σημείων
η μέση τιμή και η διάμεσος, αντίστοιχα, των τεταγμένων των σημείων  .
.Φιλικά,
Μάριος

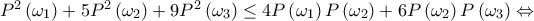
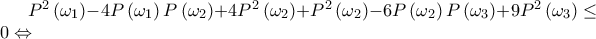

 ως άθροισμα μη αρνητικών αριθμών.
ως άθροισμα μη αρνητικών αριθμών.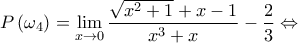






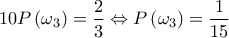
 παίρνουμε
παίρνουμε  και
και 
 άρα τα
άρα τα 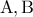 δεν είναι ασυμβίβαστα.
δεν είναι ασυμβίβαστα.
 είναι βέβαιο οπότε το αντίθετο του είναι αδύνατο.
είναι βέβαιο οπότε το αντίθετο του είναι αδύνατο.![P\left( \Gamma \right) = \left[ {\left( {{\rm A} \cap {\rm B}} \right) \cup {{\left( {{\rm A} \cup {\rm B}} \right)}^\prime }} \right] = P\left( {A \cap B} \right) + P\left[ {{{\left( {A \cup B} \right)}^\prime }} \right] = P\left( {{\omega _2}} \right) + 0 = \dfrac{1}{5} P\left( \Gamma \right) = \left[ {\left( {{\rm A} \cap {\rm B}} \right) \cup {{\left( {{\rm A} \cup {\rm B}} \right)}^\prime }} \right] = P\left( {A \cap B} \right) + P\left[ {{{\left( {A \cup B} \right)}^\prime }} \right] = P\left( {{\omega _2}} \right) + 0 = \dfrac{1}{5}](/forum/ext/geomar/texintegr/latexrender/pictures/bb73cf40fee6ed7a9c638fa640a1615a.png)
![P\left( \Delta \right) = P\left[ {{{\left( {A \cap B} \right)}^\prime }} \right] = P\left[ {{{\left( {{\omega _2}} \right)}^\prime }} \right] = 1 - \dfrac{1}{5} = \dfrac{4}{5} P\left( \Delta \right) = P\left[ {{{\left( {A \cap B} \right)}^\prime }} \right] = P\left[ {{{\left( {{\omega _2}} \right)}^\prime }} \right] = 1 - \dfrac{1}{5} = \dfrac{4}{5}](/forum/ext/geomar/texintegr/latexrender/pictures/e5c2ec1c0c796b84bec67097509ab875.png)

 ,
,  και
και 

 επομένως η διάμεσος τους είναι:
επομένως η διάμεσος τους είναι:
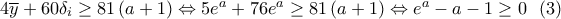



 είναι γνησίως αύξουσα στο διάστημα
είναι γνησίως αύξουσα στο διάστημα  και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο ![\left( { - \infty ,0} \right] \left( { - \infty ,0} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/b8ca05bb5238a874a6434ebf5713206d.png) και παρουσιάζει ελάχιστο για
και παρουσιάζει ελάχιστο για  το
το  ,
, ισχύει
ισχύει  δηλαδή ισχύει η σχέση
δηλαδή ισχύει η σχέση 