 για τις οποίες ισχύει
για τις οποίες ισχύει 
για κάθε

Συντονιστές: achilleas, emouroukos, silouan
 για τις οποίες ισχύει
για τις οποίες ισχύει 


 η δεύτερη δίνει ότι
η δεύτερη δίνει ότι 



 (και πολλές άλλες άχρηστες σχέσεις)
(και πολλές άλλες άχρηστες σχέσεις) είναι το μηδενικό αφού έχει άπειρες ρίζες)
είναι το μηδενικό αφού έχει άπειρες ρίζες) η
η  δίνει
δίνει 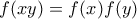
 που ικανοποιεί τις
που ικανοποιεί τις 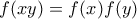 και
και  και
και 

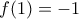 τότε η
τότε η  ικανοποιεί το 2)
ικανοποιεί το 2)
 τότε
τότε 



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες