 είναι θετικοί τέτοιοι ώστε να μπορούν να γίνουν πλευρές τριγώνου και να επαληθεύουν την σχέση
είναι θετικοί τέτοιοι ώστε να μπορούν να γίνουν πλευρές τριγώνου και να επαληθεύουν την σχέση  . Να αποδείξετε
. Να αποδείξετε ![\frac{2x+y}{\sqrt{x+z}}+\frac{2y+z}{\sqrt{y+x}}+\frac{2z+x}{\sqrt{z+y}}\geq 6\sqrt{2}\sqrt[6]{zx+yz+xy-xyz-1} \frac{2x+y}{\sqrt{x+z}}+\frac{2y+z}{\sqrt{y+x}}+\frac{2z+x}{\sqrt{z+y}}\geq 6\sqrt{2}\sqrt[6]{zx+yz+xy-xyz-1}](/forum/ext/geomar/texintegr/latexrender/pictures/5865cd7b37d20c33cb7051b8dff2bdbf.png)
Συντονιστές: achilleas, emouroukos, silouan
 είναι θετικοί τέτοιοι ώστε να μπορούν να γίνουν πλευρές τριγώνου και να επαληθεύουν την σχέση
είναι θετικοί τέτοιοι ώστε να μπορούν να γίνουν πλευρές τριγώνου και να επαληθεύουν την σχέση  . Να αποδείξετε
. Να αποδείξετε ![\frac{2x+y}{\sqrt{x+z}}+\frac{2y+z}{\sqrt{y+x}}+\frac{2z+x}{\sqrt{z+y}}\geq 6\sqrt{2}\sqrt[6]{zx+yz+xy-xyz-1} \frac{2x+y}{\sqrt{x+z}}+\frac{2y+z}{\sqrt{y+x}}+\frac{2z+x}{\sqrt{z+y}}\geq 6\sqrt{2}\sqrt[6]{zx+yz+xy-xyz-1}](/forum/ext/geomar/texintegr/latexrender/pictures/5865cd7b37d20c33cb7051b8dff2bdbf.png)
Κάτι δεν πάει καλά: ΓιαXriiiiistos έγραψε: ↑Πέμ Αύγ 16, 2018 3:58 pmOι αριθμοίείναι θετικοί τέτοιοι ώστε να μπορούν να γίνουν πλευρές τριγώνου και να επαληθεύουν την σχέση
. Να αποδείξετε
 , η υπόρριζη ποσότητα
, η υπόρριζη ποσότητα  είναι αρνητική...
είναι αρνητική...Πράγματι κάτι δεν πάει αλλάMihalis_Lambrou έγραψε: ↑Πέμ Αύγ 16, 2018 5:24 pmΚάτι δεν πάει καλά: ΓιαXriiiiistos έγραψε: ↑Πέμ Αύγ 16, 2018 3:58 pmOι αριθμοίείναι θετικοί τέτοιοι ώστε να μπορούν να γίνουν πλευρές τριγώνου και να επαληθεύουν την σχέση
. Να αποδείξετε
, η υπόρριζη ποσότητα
είναι αρνητική...
 ... Το πρόβλημα είναι ότι θέτοντας
... Το πρόβλημα είναι ότι θέτοντας  δεν έχουμε ισότητα...
δεν έχουμε ισότητα... είναι πλευρές τριγώνου μπορούμε να θέσουμε
είναι πλευρές τριγώνου μπορούμε να θέσουμε  ,
,  ,
,  και θα ικανοποιείται πάντα η τριγωνική ανισότητα.
και θα ικανοποιείται πάντα η τριγωνική ανισότητα. και κάνοντας λίγες πράξεις προκύπτει ότι αρκεί να αποδείξουμε ότι:
και κάνοντας λίγες πράξεις προκύπτει ότι αρκεί να αποδείξουμε ότι:![\dfrac{1+a+2b}{\sqrt{1+a}}+\dfrac{1+b+2c}{\sqrt{1+b}}+\dfrac{1+c+2a}{\sqrt{1+c}}\geq 6\sqrt{2}\sqrt[6]{a^2+b^2+c^2+3(ab+bc+ca)-1-ab(a+b)-bc(b+c)-ca(c+a)-2abc}\Leftrightarrow \dfrac{1+a+2b}{\sqrt{1+a}}+\dfrac{1+b+2c}{\sqrt{1+b}}+\dfrac{1+c+2a}{\sqrt{1+c}}\geq 6\sqrt{2}\sqrt[6]{a^2+b^2+c^2+3(ab+bc+ca)-1-ab(a+b)-bc(b+c)-ca(c+a)-2abc}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/d8784da916bdf278dc6dbcdc9c220e8b.png)
![\dfrac{1+a+2b}{\sqrt{1+a}}+\dfrac{1+b+2c}{\sqrt{1+b}}+\dfrac{1+c+2a}{\sqrt{1+c}}\geq 6\sqrt{2}\sqrt[6]{ab+bc+ca-ab(a+b)-bc(b+c)-ca(c+a)-2abc}\Leftrightarrow \dfrac{1+a+2b}{\sqrt{1+a}}+\dfrac{1+b+2c}{\sqrt{1+b}}+\dfrac{1+c+2a}{\sqrt{1+c}}\geq 6\sqrt{2}\sqrt[6]{ab+bc+ca-ab(a+b)-bc(b+c)-ca(c+a)-2abc}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/59536e4c3d1e12674f4772ae3da51d15.png) (*)
(*)![\dfrac{1+a+2b}{\sqrt{1+a}}+\dfrac{1+b+2c}{\sqrt{1+b}}+\dfrac{1+c+2a}{\sqrt{1+c}}\geq 6\sqrt{2}\sqrt[6]{abc} \dfrac{1+a+2b}{\sqrt{1+a}}+\dfrac{1+b+2c}{\sqrt{1+b}}+\dfrac{1+c+2a}{\sqrt{1+c}}\geq 6\sqrt{2}\sqrt[6]{abc}](/forum/ext/geomar/texintegr/latexrender/pictures/84a505db2565acdd0a5ff50917239f28.png) .
. , επομένως αρκεί:
, επομένως αρκεί:![2\sqrt{2a}+2\sqrt{2b}+2\sqrt{2c}\geq 6\sqrt{2}\sqrt[6]{abc}\Leftrightarrow \sqrt{a}+\sqrt{b}+\sqrt{c}\geq 3\sqrt[6]{abc} 2\sqrt{2a}+2\sqrt{2b}+2\sqrt{2c}\geq 6\sqrt{2}\sqrt[6]{abc}\Leftrightarrow \sqrt{a}+\sqrt{b}+\sqrt{c}\geq 3\sqrt[6]{abc}](/forum/ext/geomar/texintegr/latexrender/pictures/40e0f4fa8a491b2f00e840108ad6dda4.png) που ισχύει από
που ισχύει από  .
. ,
,  ,
,  το
το  ,
, 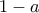 ,
,  .
.Με τον τρόπο που χρησιμοποίησα παραπάνω φτάνουμε στο:
![\dfrac{1+a+2b}{\sqrt{1+a}}+\dfrac{1+b+2c}{\sqrt{1+b}}+\dfrac{1+c+2a}{\sqrt{1+c}}\geq 9\sqrt[6]{abc} \dfrac{1+a+2b}{\sqrt{1+a}}+\dfrac{1+b+2c}{\sqrt{1+b}}+\dfrac{1+c+2a}{\sqrt{1+c}}\geq 9\sqrt[6]{abc}](/forum/ext/geomar/texintegr/latexrender/pictures/09ca73a8b6037fe8b838666607fd01a6.png) με
με  .
. στο αριστερό μέλος αρκεί να αποδειχθεί τώρα ότι:
στο αριστερό μέλος αρκεί να αποδειχθεί τώρα ότι:![3\sqrt[3]{\dfrac{(1+a+2b)(1+b+2c)(1+c+2a)}{\sqrt{(a+1)(b+1)(c+1)}}}\geq 9\sqrt[6]{abc}\Leftrightarrow (1+a+2b)(1+b+2c)(1+c+2a)\geq 3\sqrt[3]{\dfrac{(1+a+2b)(1+b+2c)(1+c+2a)}{\sqrt{(a+1)(b+1)(c+1)}}}\geq 9\sqrt[6]{abc}\Leftrightarrow (1+a+2b)(1+b+2c)(1+c+2a)\geq](/forum/ext/geomar/texintegr/latexrender/pictures/135d177018c53e5e2a957c0448fc30dd.png)

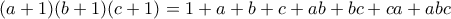 .
. , δηλαδή
, δηλαδή  και
και ![a+b+c\geq 3\sqrt[3]{abc} a+b+c\geq 3\sqrt[3]{abc}](/forum/ext/geomar/texintegr/latexrender/pictures/d4d554afa10b5764f742ffc096c0181d.png) , δηλαδή
, δηλαδή  , προκύπτει ότι
, προκύπτει ότι  .
.
 πως
πως ![1+a+2b=\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}+a+b+b\geq 6\sqrt[6]{\dfrac{1}{27}ab^2} 1+a+2b=\dfrac{1}{3}+\dfrac{1}{3}+\dfrac{1}{3}+a+b+b\geq 6\sqrt[6]{\dfrac{1}{27}ab^2}](/forum/ext/geomar/texintegr/latexrender/pictures/97c0cb9e270182dcffdf5fc5524c499d.png)
 και
και  και πολλαπλασιάζοντας κατά μέλη προκύπτει ότι:
και πολλαπλασιάζοντας κατά μέλη προκύπτει ότι:![(1+a+2b)(1+b+2c)(1+c+2a)\geq 6^3\sqrt[6]{\dfrac{1}{27^3}a^3b^3c^3}=6^3\sqrt{\dfrac{1}{27}abc}=8\cdot 27\sqrt{\dfrac{1}{27}abc}=27\sqrt{\dfrac{64}{27}abc} (1+a+2b)(1+b+2c)(1+c+2a)\geq 6^3\sqrt[6]{\dfrac{1}{27^3}a^3b^3c^3}=6^3\sqrt{\dfrac{1}{27}abc}=8\cdot 27\sqrt{\dfrac{1}{27}abc}=27\sqrt{\dfrac{64}{27}abc}](/forum/ext/geomar/texintegr/latexrender/pictures/a22ef0f69d8da6757099dd6e36d46374.png) και το ζητούμενο έπεται.
και το ζητούμενο έπεται. , δηλαδή όταν
, δηλαδή όταν  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες