 ώστε
ώστε  και πραγματικός
και πραγματικός  . Να δείξετε ότι
. Να δείξετε ότι ![a+b+c+k\geq 9\sqrt[3]{bc\frac{k-a-b-c}{3}} a+b+c+k\geq 9\sqrt[3]{bc\frac{k-a-b-c}{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/cbaf848ea7f77d0b1e339d4a272964fd.png)
Συντονιστές: achilleas, emouroukos, silouan
 και
και  για κάποιο
για κάποιο  που θα επιλέξω αργότερα. Τότε
που θα επιλέξω αργότερα. Τότε  και
και  . Επίσης
. Επίσης
![\displaystyle 9\sqrt[3]{bc \frac{k-a-b-c}{3}} = 9\sqrt[3]{N^2 \frac{2N}{3}} = 9\sqrt[3]{\frac{2}{3}}N \displaystyle 9\sqrt[3]{bc \frac{k-a-b-c}{3}} = 9\sqrt[3]{N^2 \frac{2N}{3}} = 9\sqrt[3]{\frac{2}{3}}N](/forum/ext/geomar/texintegr/latexrender/pictures/410a23f1875c1582d7694522d902e7e2.png)
 αρκετά μεγάλο. Π.χ. για
αρκετά μεγάλο. Π.χ. για  έχουμε
έχουμε  και
και ![\displaystyle 9\sqrt[3]{bc \frac{k-a-b-c}{3}} = 78.622\ldots. \displaystyle 9\sqrt[3]{bc \frac{k-a-b-c}{3}} = 78.622\ldots.](/forum/ext/geomar/texintegr/latexrender/pictures/fe5eeb57bd4bc4996e8b12dcee3ce6b2.png)
 ώστε
ώστε  και
και  να δείξετε ότι
να δείξετε ότι ![a+b+c+k\geq 9\sqrt[3]{\frac{k-a-b-c}{3}bc} a+b+c+k\geq 9\sqrt[3]{\frac{k-a-b-c}{3}bc}](/forum/ext/geomar/texintegr/latexrender/pictures/74f6eb0053f5c476ea24e3b487c1bfb1.png)
Xriiiiistos έγραψε: ↑Τρί Δεκ 04, 2018 4:03 pmΗ άσκηση αυτήν την φορά είναι επιβεβαιωμένα σωστή
Δίνονται αριθμοίώστε
και
να δείξετε ότι
![a+b+c+k\geq 9\sqrt[3]{\frac{k-a-b-c}{3}bc} a+b+c+k\geq 9\sqrt[3]{\frac{k-a-b-c}{3}bc}](/forum/ext/geomar/texintegr/latexrender/pictures/74f6eb0053f5c476ea24e3b487c1bfb1.png)
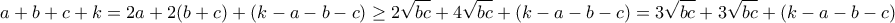
![\displaystyle{ \ge 3 \sqrt [3]{ 3\sqrt {bc} \cdot 3 \sqrt {bc} \cdot (k-a-b-c) } = 9\sqrt[3]{\frac{k-a-b-c}{3}bc}} \displaystyle{ \ge 3 \sqrt [3]{ 3\sqrt {bc} \cdot 3 \sqrt {bc} \cdot (k-a-b-c) } = 9\sqrt[3]{\frac{k-a-b-c}{3}bc}}](/forum/ext/geomar/texintegr/latexrender/pictures/52185250d1dc77f86d6eb587d093abb5.png)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες