Ανισότητα με λογάριθμο
Δημοσιεύτηκε: Πέμ Νοέμ 29, 2018 6:59 am
Ας είναι  ,
,  θετικοί αριθμοί διαφορετικοί του
θετικοί αριθμοί διαφορετικοί του  τέτοιοι ώστε
τέτοιοι ώστε 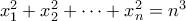 . Αποδείξατε ότι:
. Αποδείξατε ότι:

 ,
,  θετικοί αριθμοί διαφορετικοί του
θετικοί αριθμοί διαφορετικοί του  τέτοιοι ώστε
τέτοιοι ώστε 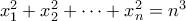 . Αποδείξατε ότι:
. Αποδείξατε ότι:
https://www.mathematica.gr/forum/
https://www.mathematica.gr/forum/viewtopic.php?f=180&t=63168
 ,
,  θετικοί αριθμοί διαφορετικοί του
θετικοί αριθμοί διαφορετικοί του  τέτοιοι ώστε
τέτοιοι ώστε 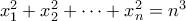 . Αποδείξατε ότι:
. Αποδείξατε ότι:
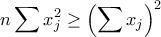
 (
( )
)

![\displaystyle{\begin{aligned}
\sum \frac{\log_{x_1}^4 x_2}{x_1+x_2} & \geq \frac{\left (\sum \log_{x_1}^2 x_2 \right )^2}{\sum (x_1+x_2)} \\
&= \frac{\left ( \sum \log_{x_1}^2 x_2 \right )^2}{2\sum x_1} \\
&\!\!\!\!\!\!\overset{\text{AM-GM}}{\geq } \frac{\left [ n \left (\prod \log_{x_1} x_2 \right )^{2/n} \right ]^2}{2\sum x_1} \\
&\!\!\!\!\overset{\text{C-B-S}}{\geq } \frac{n^2}{2n^2} \\
&= \frac{1}{2}
\end{aligned}} \displaystyle{\begin{aligned}
\sum \frac{\log_{x_1}^4 x_2}{x_1+x_2} & \geq \frac{\left (\sum \log_{x_1}^2 x_2 \right )^2}{\sum (x_1+x_2)} \\
&= \frac{\left ( \sum \log_{x_1}^2 x_2 \right )^2}{2\sum x_1} \\
&\!\!\!\!\!\!\overset{\text{AM-GM}}{\geq } \frac{\left [ n \left (\prod \log_{x_1} x_2 \right )^{2/n} \right ]^2}{2\sum x_1} \\
&\!\!\!\!\overset{\text{C-B-S}}{\geq } \frac{n^2}{2n^2} \\
&= \frac{1}{2}
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/9e81fb7e13a2fcbf8d5fc06d12efbf7b.png)