Χριστουγεννιάτικη

JimNt. · #1

Να βρεθούν όλες οι $f: \mathbb{Z^{+}} \rightarrow \mathbb{Z^{+}}$ ώστε για κάθε ζεύγος θετικών ακεραίων να ισχύει ότι xf(x)+y|f(x)^2+f(y)

. Για μαθητές μέχρι την Τετάρτη.

min## · #2

Αν βάλω όπου

το

προκύπτει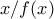

για κάθε

.Έτσι,η

παίρνει θερινές ακέραιες τιμές.Αντικαθιστώντας στην αρχική,έχω x^2g(x)+y/x^2g(x)^2+yg(y)

ή

.Αν τύχει και ισχύει x^2g(x)+y>y(g(x)-g(y))

και

για κάποια x,y

θα ισχύει απαραίτητα g(x)=g(y)

.Κρατώντας σταθερό το

,οι ανισότητες ισχύουν για αρκετά μεγάλα

(λόγω του ότι η

είναι κάτω φραγμένη)
,οπότε και για αρκετά μεγάλα

(συναληθεύοντας) θα ισχύει g(x)=g(1)=g(2)=..

και τελικά g(x)=c

για κάθε

,δηλαδή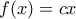

για κάθε

,που επαληθεύει..

JimNt. · #3

Διονύσιος Αδαμόπουλος · #4

Θέτοντας

παίρνουμε ότι $xf(x)+x|f(x)^2+f(x)\Leftrightarrow x(f(x)+1)|f(x)(f(x)+1)\Leftrightarrow x|f(x)$ .

Έστω λοιπόν $f(x)=g(x)\cdot x$ , όπου g(x)

μια συνάρτηση από τους θετικούς ακεραίους στους θετικούς ακεραίους.

Θέτουμε στην αρχική y=1

. Έχουμε ότι:

$xf(x)+1|f(x)^2+f(1)\Leftrightarrow xf(x)+1|f(x)^2+f(1)-g(x)(xf(x)+1)\Leftrightarrow$

$\Leftrightarrow xf(x)+1|f(1)-g(x)\Leftrightarrow g(x)x^2+1|f(1)-g(x)$

Παρατηρούμε πως πρέπει είτε f(1)=g(x)

, είτε $|f(1)-g(x)|\geq g(x)x^2+1$ .

Aν f(1)<g(x)

, για κάποιο

, τότε $g(x)-f(1)\geq g(x)x^2+1\Leftrightarrow 0\geq g(x)(x^2-1)+f(1)+1$ , άτοπο, αφού g(x)>0

,

, $χ^2\geq 1$ .

Έστω πως f(1)>g(x)

, για κάποιο

. Τότε θα έπρεπε $f(1)-g(x)\geq g(x)x^2+1\Leftrightarrow f(1)\geq g(x)(x^2+1)+1$ .

Αυτό όμως δεν μπορεί να γίνεται για αρκετά μεγάλα

, καθώς το g(x)(x^2+1)+1

δεν φράζεται.

Συνεπώς για αρκετά μεγάλα

, είναι

. Δηλαδή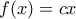

, όπου

, για πολύ μεγάλα

.

Θέτουμε στην αρχική ένα μεγάλο

και έχουμε ότι:

$cx^2+y|c^2x^2+g(y)y\Leftrightarrow cx^2+y|c^2x^2+g(y)y-c(cx^2+y)\Leftrightarrow cx^2+y|y(g(y)-c)$ , για ένα μεγάλο

και για κάθε

.

Έστω $g(y)\ne c$ .

Κρατώντας το

σταθερό και μεγιστοποιώντας το

παρατηρούμε πως πρέπει κάτι μη φραγμένο να διαιρεί κάτι πεπερασμένο και διάφορο του μηδενός, οπότε για κάποιο πάρα πολύ μεγάλο

έχουμε άτοπο. Συνεπώς g(x)=c

και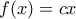

για κάθε θετικό ακέραιο

, όπου

.

Edit: Με πρόλαβαν!

Χριστουγεννιάτικη

Χριστουγεννιάτικη

Re: Χριστουγεννιάτικη

Re: Χριστουγεννιάτικη

Re: Χριστουγεννιάτικη

Μέλη σε σύνδεση