 με
με  και
και  πραγματικοί αριθμοί τέτοιοι, ώστε
πραγματικοί αριθμοί τέτοιοι, ώστε  .
. Να αποδείξετε ότι:

Συντονιστές: achilleas, emouroukos, silouan
 με
με  και
και  πραγματικοί αριθμοί τέτοιοι, ώστε
πραγματικοί αριθμοί τέτοιοι, ώστε  .
. 
 , και μάλιστα η περίπτωση αυτή ουσιαστικά επιλύει το πρόβλημα (ένεκα μαθηματικής επαγωγής)!
, και μάλιστα η περίπτωση αυτή ουσιαστικά επιλύει το πρόβλημα (ένεκα μαθηματικής επαγωγής)! λοιπόν η πρόταση είναι: αν
λοιπόν η πρόταση είναι: αν  και
και  τότε
τότε  .
. στην
στην  λαμβάνουμε την
λαμβάνουμε την  , που ισχύει. (Αν
, που ισχύει. (Αν  τότε
τότε  , ενώ η
, ενώ η  είναι δεδομένη.)
είναι δεδομένη.) με
με  ,
,  ,
,  . Παρατηρούμε ότι ισχύουν οι
. Παρατηρούμε ότι ισχύουν οι  και
και  ,
, 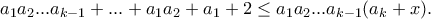 (*)
(*)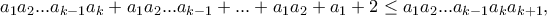
 (**)
(**) , που είναι προφανής.
, που είναι προφανής. ...).
...). θέτουμε
θέτουμε  . Με εφαρμογή της ανισότητας Chebyshev για τις όμοια διατεταγμένες
. Με εφαρμογή της ανισότητας Chebyshev για τις όμοια διατεταγμένες  -άδες
-άδες 





Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες