Λάμπρος Κατσάπας έγραψε: ↑Τετ Ιουν 03, 2020 9:43 pm
It depends on the context όπως λένε και οι Εγγλέζοι. Εξαρτάται από το πλαίσιο στο οποίο βρισκόμαστε. Οι Άγγλοι χρησιμοποιούν δύο διαφορετικές ορολογίες για το ''τυχαίο σημείο''. Arbitrary point ή Random point. Στο δεύτερο υποβόσκει η κατανομή από την οποία προέρχεται το σημείο και χρησιμοποιείται σε προβλήματα πιθανοτήτων.
Οι λέξεις Arbitrary και Random είναι δύο διαφορετικές λέξεις με διαφορετική ρίζα. Οι λέξεις όμως "τυχαίος" και "τυχών" είναι έννοιες ταυτόσημες και δεν υπάρχει κανένας διαχωρισμός. Απλώς η πρώτη είναι επίθετο της Νεοελληνικής γλώσσας και η δεύτερη μετοχής της Αρχαίας Ελληνικής.
Λάμπρος Κατσάπας έγραψε: ↑Τετ Ιουν 03, 2020 9:43 pm
Η διάκριση αυτή υπάρχει και στα ελληνικά βιβλία όπως έχω παρατηρήσει με το Arbitrary point να μεταφράζεται ως τυχόν σημείο και το Random point για το τυχαίο σημείο.
Εγώ αυτή τη διάκριση δεν την έχω δει πουθενά. Χρησιμοποιούνται εξίσου και τα δύο όταν πρόκειται για γεωμετρικά προβλήματα. Έχω πάμπολλα τέτοια παραδείγματα από διάφορα βιβλία Γεωμετρίας, αλλά θα αρκεστώ στο σχολικό βιβλίο. Ενδεικτικά αναφέρω:
Ευκλείδεια Γεωμετρία Α λυκείου.
Σελίδα 28 Αποδεικτικές ασκήσεις 2) Θεωρούμε κυρτή γωνία

τη διχοτόμο
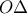
και
τυχαία ημιευθεία 
Σελίδα 37 Γενικές Ασκήσεις 5) Δίνεται ημικύκλιο διαμέτρου

,

το μέσο του τόξου

και
 τυχαίο σημείο
τυχαίο σημείο του τόξου.
Ευκλείδεια Γεωμετρία Β λυκείου.
Σελίδα 19 Ασκήσεις Εμπέδωσης 7) Από
τυχαίο σημείο 
της διαμέσου...
Σελίδα 23 (Απολλώνιος Κύκλος) Έστω δύο δεδομένα σημεία

και
 τυχαίο σημείο
τυχαίο σημείο του τόπου.
 ενός κύκλου
ενός κύκλου  κατασκευάζουμε ορθογώνιο τρίγωνο
κατασκευάζουμε ορθογώνιο τρίγωνο  με κάθετες πλευρές
με κάθετες πλευρές (τα σημεία
(τα σημεία  είναι εσωτερικά του κύκλου). Αν
είναι εσωτερικά του κύκλου). Αν  είναι τυχαίο σημείο του κύκλου, να
είναι τυχαίο σημείο του κύκλου, να  και να διαπιστώσετε ότι το άθροισμά τους είναι
και να διαπιστώσετε ότι το άθροισμά τους είναι 




 διατρέχει το
διατρέχει το  το
το  και το
και το 
 τότε
τότε 

 το μέσο της
το μέσο της  και
και  η προβολή του
η προβολή του  τότε το δεύτερο θεώρημα των διαμέσων με προσανατολισμό
τότε το δεύτερο θεώρημα των διαμέσων με προσανατολισμό


 τη διχοτόμο
τη διχοτόμο 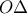 και
και 
 και
και 
 και έχω
και έχω 
 όπου με τη βοήθεια παραγώγων
όπου με τη βοήθεια παραγώγων  για
για  και ελάχιστη τιμή
και ελάχιστη τιμή  για
για 
 το μέσο του
το μέσο του 

 παράσταση που δεν εξαρτάτε από το
παράσταση που δεν εξαρτάτε από το  φαίνονται τα συμπεράσματα από τη λύση μου,
φαίνονται τα συμπεράσματα από τη λύση μου, 
 είναι τα σημεία όπου η παράσταση
είναι τα σημεία όπου η παράσταση  παίρνει την ελάχιστη και τη μέγιστη τιμή αντίστοιχα.
παίρνει την ελάχιστη και τη μέγιστη τιμή αντίστοιχα. είναι τα σημεία όπου η παράσταση
είναι τα σημεία όπου η παράσταση  παίρνει τη μέγιστη και την ελάχιστη τιμή αντίστοιχα.
παίρνει τη μέγιστη και την ελάχιστη τιμή αντίστοιχα.