 για την οποία ισχύει:
για την οποία ισχύει:
Συντονιστές: achilleas, emouroukos, silouan
 (1)
(1) :
: 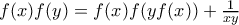 (2)
(2) (3)
(3)
 :
:  (4)
(4) :
:  (5)
(5) (6)
(6) :
: 
 και
και  :
:
 και
και 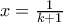 :
:
 και
και  :
: 
 :
: 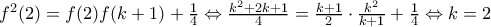

 :
: 
 :
: 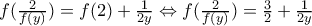
 , εύκολα προκύπτει ότι :
, εύκολα προκύπτει ότι :  , η οποία για
, η οποία για  δίνει
δίνει
 , η οποία επαληθεύει.
, η οποία επαληθεύει.Έστω
 :
: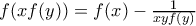
 :
: (1)
(1)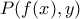 :
:
 στην τελευταία έχουμε:
στην τελευταία έχουμε:
 (2)
(2) στην τελευταία έχουμε:
στην τελευταία έχουμε: .
. στην τελευταία έχουμε:
στην τελευταία έχουμε: 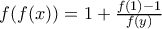 (3)
(3)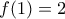 και αρα
και αρα 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες