 θετικοί αριθμοί με
θετικοί αριθμοί με  . Να αποδειχθεί ότι
. Να αποδειχθεί ότι 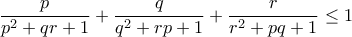
Συντονιστές: achilleas, emouroukos, silouan
Μη αναγνωσμένη δημοσίευση από Mihalis_Lambrou » Σάβ Φεβ 24, 2024 5:39 pm
 θετικοί αριθμοί με
θετικοί αριθμοί με  . Να αποδειχθεί ότι
. Να αποδειχθεί ότι 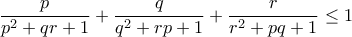
Μη αναγνωσμένη δημοσίευση από vgreco » Κυρ Φεβ 25, 2024 4:21 pm
Έχουμε:
![\displaystyle{
\begin{aligned}
\sum \dfrac{p}{p^2 + qr + 1}
&\le \sum \dfrac{p}{2p + qr} \\[0.06in]
&= \dfrac{1}{2} \sum \dfrac{2p}{2p + qr} \\[0.06in]
&= \dfrac{1}{2} \sum \biggl( 1 - \dfrac{qr}{2p + qr} \biggr) \\[0.06in]
&= \dfrac{3}{2} - \dfrac{1}{2}\sum \dfrac{ \bigl( qr \bigr)^2 }{2pqr + \bigl( qr \bigr)^2} \\[0.06in]
&\le \dfrac{3}{2} - \dfrac{1}{2} \cdot \dfrac{ \bigl( pq + qr + rp \bigr)^2}{p^2q^2 + q^2r^2 + r^2p^2 + 6pqr} \\[0.06in]
&= \dfrac{3}{2} - \dfrac{1}{2} \cdot 1 = 1
\end{aligned}
} \displaystyle{
\begin{aligned}
\sum \dfrac{p}{p^2 + qr + 1}
&\le \sum \dfrac{p}{2p + qr} \\[0.06in]
&= \dfrac{1}{2} \sum \dfrac{2p}{2p + qr} \\[0.06in]
&= \dfrac{1}{2} \sum \biggl( 1 - \dfrac{qr}{2p + qr} \biggr) \\[0.06in]
&= \dfrac{3}{2} - \dfrac{1}{2}\sum \dfrac{ \bigl( qr \bigr)^2 }{2pqr + \bigl( qr \bigr)^2} \\[0.06in]
&\le \dfrac{3}{2} - \dfrac{1}{2} \cdot \dfrac{ \bigl( pq + qr + rp \bigr)^2}{p^2q^2 + q^2r^2 + r^2p^2 + 6pqr} \\[0.06in]
&= \dfrac{3}{2} - \dfrac{1}{2} \cdot 1 = 1
\end{aligned}
}](/forum/ext/geomar/texintegr/latexrender/pictures/f23dd90d8564db212b8228618082b60a.png)
 . Η ισότητα ισχύει μόνο αν
. Η ισότητα ισχύει μόνο αν  .
.Επιστροφή σε “Άλγεβρα - Επίπεδο Αρχιμήδη (Seniors)”
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off