Αντιρρόπως ίσα τρίγωνα
Δημοσιεύτηκε: Τρί Νοέμ 01, 2016 7:01 pm
Θεωρούμε τα τρίγωνα 
τα οποία είναι αντιρρόπως ίσα.
(δυο τρίγωνα είναι αντιρρόπως ίσα αν στο επίπεδο κάνοντας μια στροφή, μια συμμετρία ως προς ευθεία και μια μεταφορά
μπορούμε να φέρουμε το ένα πάνω στο άλλο.Ενω είναι ομορρόπως ίσα αν στο επίπεδο κάνοντας μια στροφή και μια μεταφορά
μπορούμε να φέρουμε το ένα πάνω στο άλλο . )
Να αποδειχθεί ότι τα μέσα των
βρίσκονται στην ίδια ευθεία.

τα οποία είναι αντιρρόπως ίσα.
(δυο τρίγωνα είναι αντιρρόπως ίσα αν στο επίπεδο κάνοντας μια στροφή, μια συμμετρία ως προς ευθεία και μια μεταφορά
μπορούμε να φέρουμε το ένα πάνω στο άλλο.Ενω είναι ομορρόπως ίσα αν στο επίπεδο κάνοντας μια στροφή και μια μεταφορά
μπορούμε να φέρουμε το ένα πάνω στο άλλο . )
Να αποδειχθεί ότι τα μέσα των

βρίσκονται στην ίδια ευθεία.




 .
. τα μέσα των
τα μέσα των  και ας είναι
και ας είναι  τα συμμετρικά των
τα συμμετρικά των  ως προς το
ως προς το  .
. 

 και
και  .
.


 . Είναι
. Είναι 
 συνευθειακά και το ζητούμενο έχει αποδειχθεί.
συνευθειακά και το ζητούμενο έχει αποδειχθεί. αν χρησιμοποιήθηκε άρτιος αριθμός ανακλάσεων
αν χρησιμοποιήθηκε άρτιος αριθμός ανακλάσεων αν χρησιμοποιήθηκε περιττός αριθμός ανακλάσεων
αν χρησιμοποιήθηκε περιττός αριθμός ανακλάσεων και κάποιο
και κάποιο 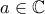 .
. με
με  , ο γεωμετρικός τόπος των σημείων που ικανοποιούν την εξίσωση
, ο γεωμετρικός τόπος των σημείων που ικανοποιούν την εξίσωση  είναι ευθεία.
είναι ευθεία. και της εικόνας του ισούται με
και της εικόνας του ισούται με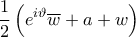
 με
με  έχουμε
έχουμε 
 και
και  είναι συνευθειακά ευθεία. Στην ίδια ευθεία μάλιστα βρίσκεται και το μέσο της
είναι συνευθειακά ευθεία. Στην ίδια ευθεία μάλιστα βρίσκεται και το μέσο της  όπου
όπου  οποιοδήποτε άλλο σημείο και
οποιοδήποτε άλλο σημείο και  η εικόνα του από τον ίδιο μετασχηματισμό.
η εικόνα του από τον ίδιο μετασχηματισμό. τα συμμετρικά του
τα συμμετρικά του  ως προς τα μέσα
ως προς τα μέσα 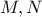 των
των  αντίστοιχα και
αντίστοιχα και  .
.  το μέσο της
το μέσο της 


 και με όμοιο τρόπο προκύπτει ότι
και με όμοιο τρόπο προκύπτει ότι  .
.

 συνευθειακά οπότε από
συνευθειακά οπότε από  προκύπτει ότι και
προκύπτει ότι και