Δεν είναι απαραίτητο τα σημεία

να ταυτίζονται με τα σημεία επαφής του εγγεγραμμένου κύκλου στις πλευρές

αντιστοίχως, του δοσμένου τριγώνου

Θα αποδειχθεί ότι ισχύει το ζητούμενο για τυχόντα σημεία

επί των

αντιστοίχως, για τα οποία όμως ισχύει


Έστω το σημείο

όπου

είναι τα ισοτομικά σημεία των

επί των πλευρών
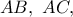
αντιστοίχως.
Έστω τα σημεία
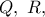
ώστε τα

να είναι παραλληλόγραμμα και έστω τα σημεία
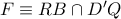
και
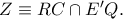
Από



Από

προκύπτει ότι το παραλληλόγραμμο

είναι ρόμβος και άρα, η διαγώνιά του

ταυτίζεται με την διχοτόμο της γωνίας

του

Τα σημεία

είναι συνευθειακά, σύμφωνα με γνωστό
Λήμμα που έχουμε ξαναδεί στο


Δείτε
Εδώ 
, λόγω του παραλληλογράμμου

με το σημείο

στο εσωτερικό του και

και


- Η τομή των παραλλήλων εκ των ισοτομικών των επαφών, επί της διχοτόμου.
- f=181_t=57751.png (31.09 KiB) Προβλήθηκε 901 φορές

Έστω

τα μέσα των

αντιστοίχως και σύμφωνα με το
Θεώρημα Gauss-Newton, έχουμε ότι τα σημεία αυτά είναι συνευθειακά.
Η ευθεία
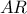
περνάει από το σημείο

λόγω του παραλληλογράμμου

Από

και

τώρα, προκύπτει

Έστω

το σημείο ώστε το

να είναι παραλληλόγραμμο και έχουμε ότι η διαγώνιά του

περνάει από το σημείο

και ισχύει
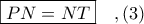
Από

και


Από


Από

προκύπτει ότι η ευθεία

ταυτίζεται με την διχοτόμο της γωνίας

του παραλληλογράμμου

Τέλος, από

και

λόγω του παραλληλογράμμου

συμπεραίνεται ότι το σημείο

ανήκει στην ευθεία

και το ζητούμενο έχει αποδειχθεί.
Κώστας Βήττας.
ΥΓ. Πράγματα, που τα έχουμε ξαναδεί αλλού, αλλά άντε βρέστα...
 τα σημεία επαφής του εγγεγραμμένου κύκλου
τα σημεία επαφής του εγγεγραμμένου κύκλου  τριγώνου
τριγώνου  με τις πλευρές του
με τις πλευρές του 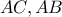 αντίστοιχα. Να δειχθεί ότι οι εκ των
αντίστοιχα. Να δειχθεί ότι οι εκ των  παράλληλες προς τις
παράλληλες προς τις  αντίστοιχα τέμνονται σε σημείο
αντίστοιχα τέμνονται σε σημείο  της διχοτόμου της γωνίας
της διχοτόμου της γωνίας  του
του  , όπου
, όπου  είναι τα ισοτομικά των
είναι τα ισοτομικά των  ως προς τις
ως προς τις 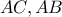 αντίστοιχα.
αντίστοιχα.
 είναι τα σημεία επαφής των παρεγγεγραμμένων κύκλων με τις αντίστοιχες πλευρές).
είναι τα σημεία επαφής των παρεγγεγραμμένων κύκλων με τις αντίστοιχες πλευρές). η διχοτόμος και
η διχοτόμος και  . Ισχύει
. Ισχύει 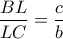 και
και  .
.  με διατέμνουσα
με διατέμνουσα  έχουμε
έχουμε 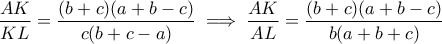 .
. το σημείο στο οποίο η παράλληλη προς την
το σημείο στο οποίο η παράλληλη προς την  τέμνει την
τέμνει την  . Τότε
. Τότε  . Άρα,
. Άρα, ![\displaystyle \frac{AM}{AL} = \frac{AM}{AK} \frac{AK}{AL} = \frac{a+c-b}{2c} \frac{(b+c)(a+b-c)}{b(a+b+c)} = \frac{(b+c)[a^2 - (b-c)^2]}{2bc(a+b+c)} \displaystyle \frac{AM}{AL} = \frac{AM}{AK} \frac{AK}{AL} = \frac{a+c-b}{2c} \frac{(b+c)(a+b-c)}{b(a+b+c)} = \frac{(b+c)[a^2 - (b-c)^2]}{2bc(a+b+c)}](/forum/ext/geomar/texintegr/latexrender/pictures/214bcbce13f1f7c21b2e0b3e8601791b.png) .
. και έτσι οι δύο παράλληλες τέμνονται επί της διχοτόμου.
και έτσι οι δύο παράλληλες τέμνονται επί της διχοτόμου. να ταυτίζονται με τα σημεία επαφής του εγγεγραμμένου κύκλου στις πλευρές
να ταυτίζονται με τα σημεία επαφής του εγγεγραμμένου κύκλου στις πλευρές  αντιστοίχως, του δοσμένου τριγώνου
αντιστοίχως, του δοσμένου τριγώνου 
 επί των
επί των 
 Έστω το σημείο
Έστω το σημείο  όπου
όπου  είναι τα ισοτομικά σημεία των
είναι τα ισοτομικά σημεία των 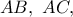 αντιστοίχως.
αντιστοίχως.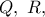 ώστε τα
ώστε τα  να είναι παραλληλόγραμμα και έστω τα σημεία
να είναι παραλληλόγραμμα και έστω τα σημεία 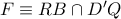 και
και 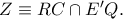



 προκύπτει ότι το παραλληλόγραμμο
προκύπτει ότι το παραλληλόγραμμο  είναι ρόμβος και άρα, η διαγώνιά του
είναι ρόμβος και άρα, η διαγώνιά του  ταυτίζεται με την διχοτόμο της γωνίας
ταυτίζεται με την διχοτόμο της γωνίας  του
του 
 είναι συνευθειακά, σύμφωνα με γνωστό
είναι συνευθειακά, σύμφωνα με γνωστό  Δείτε
Δείτε  , λόγω του παραλληλογράμμου
, λόγω του παραλληλογράμμου  με το σημείο
με το σημείο  στο εσωτερικό του και
στο εσωτερικό του και  και
και 
 τα μέσα των
τα μέσα των  αντιστοίχως και σύμφωνα με το
αντιστοίχως και σύμφωνα με το 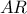 περνάει από το σημείο
περνάει από το σημείο  λόγω του παραλληλογράμμου
λόγω του παραλληλογράμμου 
 και
και  τώρα, προκύπτει
τώρα, προκύπτει 
 το σημείο ώστε το
το σημείο ώστε το  να είναι παραλληλόγραμμο και έχουμε ότι η διαγώνιά του
να είναι παραλληλόγραμμο και έχουμε ότι η διαγώνιά του  περνάει από το σημείο
περνάει από το σημείο  και ισχύει
και ισχύει 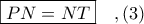
 και
και 



 προκύπτει ότι η ευθεία
προκύπτει ότι η ευθεία  ταυτίζεται με την διχοτόμο της γωνίας
ταυτίζεται με την διχοτόμο της γωνίας  του παραλληλογράμμου
του παραλληλογράμμου  και
και  λόγω του παραλληλογράμμου
λόγω του παραλληλογράμμου  συμπεραίνεται ότι το σημείο
συμπεραίνεται ότι το σημείο