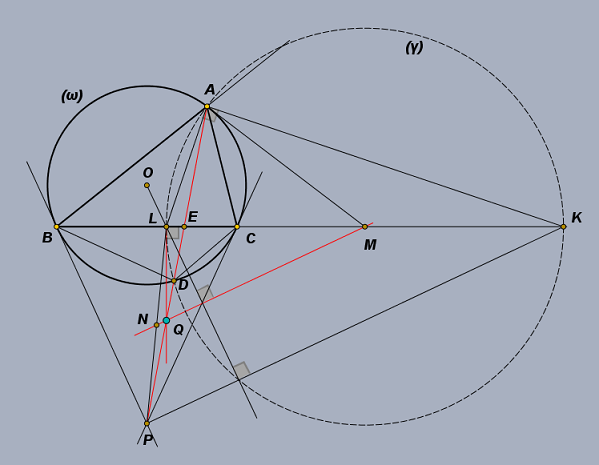
- exer19.png (83.76 KiB) Προβλήθηκε 1235 φορές
Το να δώσεις συγχαρητήρια στο Στάθη για μία λύση που έδωσε σε ένα ακόμη πρόβλημα (που ο ίδιος το χαρακτήρισε όχι πολύ δύσκολο, προσωπικά
ας μου επιτραπεί να διαφωνήσω "χαλαρά!"), το θεωρώ περιττό.
Στη συνέχεια αφού αναφέρω ότι το πρόβλημα αυτό δόθηκε στο διαγωνισμό που γίνεται στη Ρωσία προς τιμή του
μεγάλου γεωμέτρη I.F. Sharygin (1937 - 2004) τη χρονια 2015, για τις τάξεις 10-11, δίνω μια λύση που στηρίζεται στην υπόδειξη της επιτροπής του διαγωνισμού.
Εφόσον η

είναι η πολική του

ως προς τον περιγεγραμμένο κύκλο

του

, προκύπτει ότι το

ανήκει στην πολική του

.
Επίσης από το γεγονός ότι

, έχουμε ότι το

ανήκει στην πολική του

. Ως εκ τούτου η

είναι η πολική του

ως προς τον

,
οπότε λόγω ορισμού της πολικής

, και αν

,

τα μέσα των

,

αντίστοιχα, τότε

,και επομένως,

.
Όμως, από

, και εφόσον

το μέσο του

, τότε
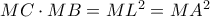
(η

διάμεσος επί την υποτείνουσα του ορθογώνιου τριγώνου

), δηλαδή, η

εφαπτομένη του

.
Από την τελευταία ισότητα προκύπτει ότι το

έχει ίσες δυνάμεις ως προς τον κύκλο

και το σημείο

, οπότε ανήκει στον ριζικό άξονα αυτών,
και εφόσον
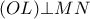
, προκύπτει ότι ο ριζικός άξονας είναι η ευθεία

.
Αρκεί να αποδείξουμε ότι το

ανήκει σε αυτόν τον άξονα.
Ο κύκλος
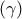
διαμέτρου

είναι ο απολλώνιος κύκλος του

, και σύμφωνα με γνωστό πρόβλημα (*) η κοινή χορδή αυτού και του

είναι
η συμμετροδιάμεσος

, που είναικαι ο ριζικός άξονας των δύο αυτών κύκλων. Το

από υπόθεση ανήκει σε αυτόν το ριζικό άξονα.
Επειδή όμως και η ευθεία

είναι ο ριζικός άξονας του κύκλου
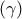
και του σημείου

, τότε το

θα είναι το κοινό σημείο των τριών ριζικών αξόνων, δηλαδή

.
(*) Αποδεικνύουμε το πρόβλημα που χρησιμοποιήσαμε.
Έστω ότι η

τέμνει τη

και τον κύκλο

στα σημεία

και

αντίστοιχα.
Τότε, από την ομοιότητα των τριγώνων
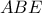
και

έχουμε :
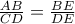
.
Από την ομοιότητα των τριγώνων

και
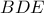
έχουμε :
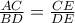
.
Με διαίρεση των δύο παραπάνω, προκύπτει ότι
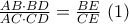
Αλλά το

είναι σημείο του απολλώνιου κύκλου , οπότε
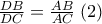
Η (1) λόγω της (2) γίνεται

, που από αυτό
προκύπτει ότι η

συμμετροδιάμεσος του
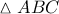
.
 και
και  τα ίχνη της εσωτερικής και εξωτερικής διχοτόμου της γωνίας
τα ίχνη της εσωτερικής και εξωτερικής διχοτόμου της γωνίας  ενός τριγώνου
ενός τριγώνου 
 αντίστοιχα. Έστω ακόμη
αντίστοιχα. Έστω ακόμη  το σημείο τομής των εφαπτομένων του περιγεγραμμένου
το σημείο τομής των εφαπτομένων του περιγεγραμμένου  του
του 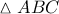 στις κορυφές
στις κορυφές  και
και  . Η κάθετος της
. Η κάθετος της  στο
στο  τέμνει την
τέμνει την  στο σημείο
στο σημείο  .
. ανήκει στην ευθεία που ενώνει τα μέσα των πλευρών
ανήκει στην ευθεία που ενώνει τα μέσα των πλευρών  και
και  του
του 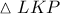 .
.
 Αν
Αν  τότε με
τότε με  την εσωτερική διχοτόμο του τριγώνου
την εσωτερική διχοτόμο του τριγώνου  προκύπτει ότι το
προκύπτει ότι το  είναι το μέσο του τόξου
είναι το μέσο του τόξου 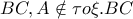 και με
και με 
 , θα είναι
, θα είναι  μεσοκάθετη της
μεσοκάθετη της 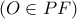 και έστω
και έστω 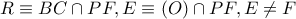 . Από
. Από  (
(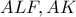
 διάμετρος του
διάμετρος του 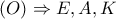 συνευθειακά.
συνευθειακά. το
το  και συνεπώς
και συνεπώς 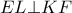 και με
και με  συνευθειακά , με
συνευθειακά , με 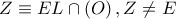 και ας είναι
και ας είναι  και
και  .
. 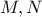 τα μέσα του τριγώνου
τα μέσα του τριγώνου 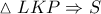 το μέσο της
το μέσο της  .
.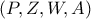 είναι αρμονική (με
είναι αρμονική (με  , και συνεπώς και η δέσμη
, και συνεπώς και η δέσμη 
 το μέσο της
το μέσο της  .
.
 .
.
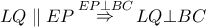 και το ισοδύναμο πρόβλημα έχει αποδειχθεί.
και το ισοδύναμο πρόβλημα έχει αποδειχθεί. όπως ορίστηκε πιο πάνω ταυτίζεται με το
όπως ορίστηκε πιο πάνω ταυτίζεται με το 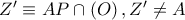 λόγω των αρμονικών σειρών
λόγω των αρμονικών σειρών  (λόγω της πολικής
(λόγω της πολικής  όπως ορίστηκε παραπάνω και
όπως ορίστηκε παραπάνω και 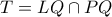 ,αρκεί
,αρκεί 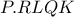 αρμονική,το οποίο είναι άμεσο επειδή
αρμονική,το οποίο είναι άμεσο επειδή 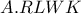
 , έχουμε ότι το
, έχουμε ότι το  είναι η πολική του
είναι η πολική του  , και αν
, και αν  ,
,  τα μέσα των
τα μέσα των  ,και επομένως,
,και επομένως,  .
. , και εφόσον
, και εφόσον 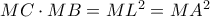
 διάμεσος επί την υποτείνουσα του ορθογώνιου τριγώνου
διάμεσος επί την υποτείνουσα του ορθογώνιου τριγώνου  εφαπτομένη του
εφαπτομένη του 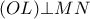 , προκύπτει ότι ο ριζικός άξονας είναι η ευθεία
, προκύπτει ότι ο ριζικός άξονας είναι η ευθεία  .
.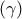 διαμέτρου
διαμέτρου  είναι ο ριζικός άξονας του κύκλου
είναι ο ριζικός άξονας του κύκλου  .
. και
και  αντίστοιχα.
αντίστοιχα.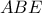 και
και  έχουμε :
έχουμε : 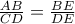 .
. και
και 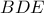 έχουμε :
έχουμε : 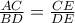 .
.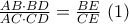
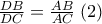
 , που από αυτό
, που από αυτό
 , άρα ανήκει στην πολική του
, άρα ανήκει στην πολική του  .
.  . Έτσι η
. Έτσι η  και επειδή και η
και επειδή και η  είναι κάθετη στην
είναι κάθετη στην 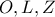 είναι συνευθειακά.
είναι συνευθειακά.  , ως προς τον δεξιά κύκλο, το
, ως προς τον δεξιά κύκλο, το  εφάπτεται του κύκλου αυτού, συμπεραίνουμε ότι η πολική του
εφάπτεται του κύκλου αυτού, συμπεραίνουμε ότι η πολική του  και η
και η  εφάπτεται στον κύκλο δεξιά. Επομένως στο ορθογώνιο τρίγωνο
εφάπτεται στον κύκλο δεξιά. Επομένως στο ορθογώνιο τρίγωνο 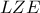 είναι
είναι  που σημαίνει ότι το
που σημαίνει ότι το 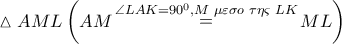
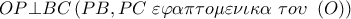
 είναι ισοσκελές, άρα
είναι ισοσκελές, άρα 




 και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.