min## έγραψε: ↑Σάβ Απρ 07, 2018 7:48 pm
Με

τις τομές της

με την

είναι και

..


- Αναπάντεχο Ισοσκελές!.png (31.02 KiB) Προβλήθηκε 826 φορές
Πράγματι:
Έστω

το σημείο στον περιγεγραμμένο κύκλο του τριγώνου του

έτσι ώστε
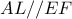
και

το αντιδιαμετρικό του

.
Παρατηρούμε πως αφού

, τα σημεία

και

θα έχουν ίσες δυνάμεις ως προς του κύκλο.
Ταυτόχρονα το τετράπλευρο

είναι παραλληλόγραμμο, αφού οι διαγώνιοι του διχοτομούνται. Άρα

, δηλαδή η δύναμη του

στον κύκλο είναι ίση με

, δηλαδή η δύναμη του

στον κύκλο είναι ίση με

. Επομένως η

είναι εφαπτόμενη στον περιγεγραμμένο κύκλο του τριγώνου

.
Ταυτόχρονα είναι

(

διάμετρος του κύκλου), δηλαδή

, λόγω του ότι
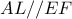
. Επομένως το

είναι το συμμετρικό του

ως προς την

και αφού η

είναι εφαπτόμενη θα είναι και η

.
Το εγγράψιμο τετράπλευρο

είναι λοιπόν αρμονικό, αφού οι εφαπτόμενες από τα

και

τέμνονται πάνω στην διαγώνιο του

, δηλαδή στο

.
Η δέσμη λοιπόν

είναι αρμονική, δηλαδή η δέσμη

είναι αρμονική. Αφού τώρα

, έχουμε πως

μέσο του

, δηλαδή

και το ζητούμενο έπεται εύκολα.
 και ο περιγεγραμμένος κύκλος του με κέντρο το
και ο περιγεγραμμένος κύκλος του με κέντρο το  . Οι εφαπτόμενες από
. Οι εφαπτόμενες από  τέμνονται στο
τέμνονται στο  . Έστω
. Έστω  το μέσο του
το μέσο του  . Η κάθετη από το
. Η κάθετη από το  στην
στην  τέμνει την εφαπτόμενη από το
τέμνει την εφαπτόμενη από το  και την
και την  στα
στα  αντίστοιχα. Να αποδειχθεί πως το τρίγωνο
αντίστοιχα. Να αποδειχθεί πως το τρίγωνο  είναι ισοσκελές.
είναι ισοσκελές.









![\begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=0.5cm,y=0.5cm]
\clip(-14.,-8.3) rectangle (11.2,6.7);
\fill[line width=0.8pt,color=white,fill=white,fill opacity=0.10000000149011612] (2.190384487963723,5.366910193221686) -- (0.,0.) -- (7.,0.) -- cycle;
\draw [line width=0.8pt,color=black] (2.190384487963723,5.366910193221686)-- (0.,0.);
\draw [line width=0.8pt,color=black] (0.,0.)-- (7.,0.);
\draw [line width=0.8pt,color=black] (7.,0.)-- (2.190384487963723,5.366910193221686);
\draw [line width=0.8pt] (3.5,1.7019865391586084) circle (1.945941814358609cm);
\draw [line width=0.8pt] (2.190384487963723,5.366910193221686)-- (3.5,-7.197471729744639);
\draw [line width=0.8pt] (2.8451922439818613,-0.9152807682614768)-- (3.5,1.7019865391586084);
\draw [line width=0.8pt] (-3.3028420336632194,3.403973078317217)-- (10.30284203366322,0.);
\draw [line width=0.8pt] (7.,0.)-- (10.30284203366322,0.);
\draw [line width=0.8pt] (3.5,-7.197471729744639)-- (7.,0.);
\draw [line width=0.8pt] (3.5,-7.197471729744639)-- (0.,0.);
\draw [line width=0.8pt] (3.5,1.7019865391586084)-- (3.5,-7.197471729744639);
\draw [line width=0.8pt] (3.5,-7.197471729744639)-- (10.30284203366322,0.);
\draw [line width=0.8pt] (2.190384487963723,5.366910193221686)-- (3.5,1.7019865391586084);
\draw [line width=0.8pt] (2.190384487963723,5.366910193221686)-- (-12.828768794504084,0.);
\draw [line width=0.8pt] (-12.828768794504084,0.)-- (0.,0.);
\draw [line width=0.8pt] (-12.828768794504084,0.)-- (3.5,-7.197471729744639);
\draw [line width=0.8pt] (-12.828768794504084,0.)-- (3.5,1.7019865391586084);
\begin{scriptsize}
\draw [fill=black] (2.190384487963723,5.366910193221686) circle (1.5pt);
\draw<span style="color:black"> (2.050907016363515,6.117590570634495) node {A};
\draw [fill=black] (0.,0.) circle (1.5pt);
\draw<span style="color:black"> (-0.532960390381481,-0.24566498328975395) node {B};
\draw [fill=black] (7.,0.) circle (1.5pt);
\draw<span style="color:black"> (7.295772200204104,-0.39992572399094795) node {C};
\draw [fill=black] (3.5,-7.197471729744639) circle (1.5pt);
\draw<span style="color:black"> (4.133427015829631,-7.148833129668182) node {D};
\draw [fill=black] (3.5,1.7019865391586084) circle (1.5pt);
\draw<span style="color:black"> (4.094861830654333,1.0655513126703942) node {O};
\draw [fill=black] (2.8451922439818613,-0.9152807682614768) circle (1.5pt);
\draw<span style="color:black"> (2.2437329422400074,-0.7855775757439326) node {M};
\draw [fill=black] (-3.3028420336632194,3.403973078317217) circle (1.5pt);
\draw<span style="color:black"> (-3.2325233526523727,4.22789649704487) node {E};
\draw [fill=black] (10.30284203366322,0.) circle (1.5pt);
\draw<span style="color:black"> (10.573812940104473,0.5642039053915141) node {F};
\draw [fill=black] (-12.828768794504084,0.) circle (1.5pt);
\draw<span style="color:black"> (-12.873819646476985,0.718464646092708) node {G};
\draw [fill=black] (2.5823578491251014,1.6063385078704626) circle (1.5pt);
\draw<span style="color:black"> (2.128037386714112,1.1812468681962898) node {H};
\draw [fill=black] (3.5,0.) circle (1.5pt);
\draw[color=black] (3.940601089953139,-0.43849090916624633) node {I};
\end{scriptsize}
\end{tikzpicture} \begin{tikzpicture}[line cap=round,line join=round,>=triangle 45,x=0.5cm,y=0.5cm]
\clip(-14.,-8.3) rectangle (11.2,6.7);
\fill[line width=0.8pt,color=white,fill=white,fill opacity=0.10000000149011612] (2.190384487963723,5.366910193221686) -- (0.,0.) -- (7.,0.) -- cycle;
\draw [line width=0.8pt,color=black] (2.190384487963723,5.366910193221686)-- (0.,0.);
\draw [line width=0.8pt,color=black] (0.,0.)-- (7.,0.);
\draw [line width=0.8pt,color=black] (7.,0.)-- (2.190384487963723,5.366910193221686);
\draw [line width=0.8pt] (3.5,1.7019865391586084) circle (1.945941814358609cm);
\draw [line width=0.8pt] (2.190384487963723,5.366910193221686)-- (3.5,-7.197471729744639);
\draw [line width=0.8pt] (2.8451922439818613,-0.9152807682614768)-- (3.5,1.7019865391586084);
\draw [line width=0.8pt] (-3.3028420336632194,3.403973078317217)-- (10.30284203366322,0.);
\draw [line width=0.8pt] (7.,0.)-- (10.30284203366322,0.);
\draw [line width=0.8pt] (3.5,-7.197471729744639)-- (7.,0.);
\draw [line width=0.8pt] (3.5,-7.197471729744639)-- (0.,0.);
\draw [line width=0.8pt] (3.5,1.7019865391586084)-- (3.5,-7.197471729744639);
\draw [line width=0.8pt] (3.5,-7.197471729744639)-- (10.30284203366322,0.);
\draw [line width=0.8pt] (2.190384487963723,5.366910193221686)-- (3.5,1.7019865391586084);
\draw [line width=0.8pt] (2.190384487963723,5.366910193221686)-- (-12.828768794504084,0.);
\draw [line width=0.8pt] (-12.828768794504084,0.)-- (0.,0.);
\draw [line width=0.8pt] (-12.828768794504084,0.)-- (3.5,-7.197471729744639);
\draw [line width=0.8pt] (-12.828768794504084,0.)-- (3.5,1.7019865391586084);
\begin{scriptsize}
\draw [fill=black] (2.190384487963723,5.366910193221686) circle (1.5pt);
\draw<span style="color:black"> (2.050907016363515,6.117590570634495) node {A};
\draw [fill=black] (0.,0.) circle (1.5pt);
\draw<span style="color:black"> (-0.532960390381481,-0.24566498328975395) node {B};
\draw [fill=black] (7.,0.) circle (1.5pt);
\draw<span style="color:black"> (7.295772200204104,-0.39992572399094795) node {C};
\draw [fill=black] (3.5,-7.197471729744639) circle (1.5pt);
\draw<span style="color:black"> (4.133427015829631,-7.148833129668182) node {D};
\draw [fill=black] (3.5,1.7019865391586084) circle (1.5pt);
\draw<span style="color:black"> (4.094861830654333,1.0655513126703942) node {O};
\draw [fill=black] (2.8451922439818613,-0.9152807682614768) circle (1.5pt);
\draw<span style="color:black"> (2.2437329422400074,-0.7855775757439326) node {M};
\draw [fill=black] (-3.3028420336632194,3.403973078317217) circle (1.5pt);
\draw<span style="color:black"> (-3.2325233526523727,4.22789649704487) node {E};
\draw [fill=black] (10.30284203366322,0.) circle (1.5pt);
\draw<span style="color:black"> (10.573812940104473,0.5642039053915141) node {F};
\draw [fill=black] (-12.828768794504084,0.) circle (1.5pt);
\draw<span style="color:black"> (-12.873819646476985,0.718464646092708) node {G};
\draw [fill=black] (2.5823578491251014,1.6063385078704626) circle (1.5pt);
\draw<span style="color:black"> (2.128037386714112,1.1812468681962898) node {H};
\draw [fill=black] (3.5,0.) circle (1.5pt);
\draw[color=black] (3.940601089953139,-0.43849090916624633) node {I};
\end{scriptsize}
\end{tikzpicture}](/forum/ext/geomar/texintegr/latexrender/pictures/98b7e9a42294237c13b05e4dc0747ee4.png)
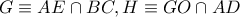 και
και  .Είναι γνωστό ότι η
.Είναι γνωστό ότι η  ως προς τον κύκλο (το
ως προς τον κύκλο (το  εγγράψιμο.Άρα
εγγράψιμο.Άρα  .Επιπλέον,
.Επιπλέον,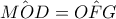 ως γωνίες με πλευρές κάθετες (είναι και οι δύο οξείες).Συμπεραίνουμε ότι
ως γωνίες με πλευρές κάθετες (είναι και οι δύο οξείες).Συμπεραίνουμε ότι  .Παρατηρούμε επίσης ότι
.Παρατηρούμε επίσης ότι  .Πράγματι,
.Πράγματι, ως παραπληρωματικές των ίσων γωνιών των ομοίων τριγώνων που αναφέραμε παραπάνω,και
ως παραπληρωματικές των ίσων γωνιών των ομοίων τριγώνων που αναφέραμε παραπάνω,και 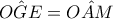 αφού το τρίγωνο
αφού το τρίγωνο  είναι ορθογώνιο,και το
είναι ορθογώνιο,και το  είναι το ύψος του.Συμπεραίνουμε λοιπόν ότι
είναι το ύψος του.Συμπεραίνουμε λοιπόν ότι  δηλαδή
δηλαδή  .Συνεπώς,η
.Συνεπώς,η  είναι μεσοκάθετος του
είναι μεσοκάθετος του  ,και το ζητούμενο έπεται.
,και το ζητούμενο έπεται. τις τομές της
τις τομές της  είναι και
είναι και  ..
..  το σημείο στον περιγεγραμμένο κύκλο του τριγώνου του
το σημείο στον περιγεγραμμένο κύκλο του τριγώνου του 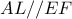 και
και  το αντιδιαμετρικό του
το αντιδιαμετρικό του  και
και  θα έχουν ίσες δυνάμεις ως προς του κύκλο.
θα έχουν ίσες δυνάμεις ως προς του κύκλο. είναι παραλληλόγραμμο, αφού οι διαγώνιοι του διχοτομούνται. Άρα
είναι παραλληλόγραμμο, αφού οι διαγώνιοι του διχοτομούνται. Άρα  , δηλαδή η δύναμη του
, δηλαδή η δύναμη του  , δηλαδή η δύναμη του
, δηλαδή η δύναμη του  είναι εφαπτόμενη στον περιγεγραμμένο κύκλο του τριγώνου
είναι εφαπτόμενη στον περιγεγραμμένο κύκλο του τριγώνου  (
( διάμετρος του κύκλου), δηλαδή
διάμετρος του κύκλου), δηλαδή  , λόγω του ότι
, λόγω του ότι  και αφού η
και αφού η  .
. είναι λοιπόν αρμονικό, αφού οι εφαπτόμενες από τα
είναι λοιπόν αρμονικό, αφού οι εφαπτόμενες από τα  είναι αρμονική, δηλαδή η δέσμη
είναι αρμονική, δηλαδή η δέσμη  είναι αρμονική. Αφού τώρα
είναι αρμονική. Αφού τώρα  , έχουμε πως
, έχουμε πως  , δηλαδή
, δηλαδή  και το ζητούμενο έπεται εύκολα.
και το ζητούμενο έπεται εύκολα.