 με
με  και ας είναι
και ας είναι  και
και  το ύψος του. Έστω το σημείο
το ύψος του. Έστω το σημείο  , όπου
, όπου  είναι το μέσον του
είναι το μέσον του  και ας είναι
και ας είναι  , η προβολή του σημείου
, η προβολή του σημείου  επί του
επί του  . Αποδείξτε ότι
. Αποδείξτε ότι  .
.Κώστας Βήττας.
Συντονιστές: vittasko, silouan, rek2
 με
με  και ας είναι
και ας είναι  και
και  το ύψος του. Έστω το σημείο
το ύψος του. Έστω το σημείο  , όπου
, όπου  είναι το μέσον του
είναι το μέσον του  και ας είναι
και ας είναι  , η προβολή του σημείου
, η προβολή του σημείου  επί του
επί του  . Αποδείξτε ότι
. Αποδείξτε ότι  .
. η αρχή ορθογωνίων συντεταγμένων με μοναδιαίο του κατακόρυφου άξονα το
η αρχή ορθογωνίων συντεταγμένων με μοναδιαίο του κατακόρυφου άξονα το 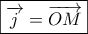 .
.  και αν
και αν  θα ισχύει :
θα ισχύει : 
 )
)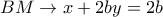 ενώ η
ενώ η  και από το σύστημά τους
και από το σύστημά τους 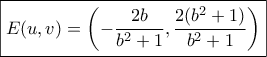 άρα ο συντελεστής διεύθυνσης της
άρα ο συντελεστής διεύθυνσης της  είναι
είναι  ενώ της
ενώ της  είναι
είναι 
 είναι η τομή των :
είναι η τομή των :  .
.  είναι
είναι  και της
και της  είναι:
είναι: 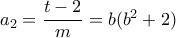 άρα
άρα 
Καλήν εσπέρα άρχοντες και καλή σας χρονιά!!!. Ας δούμε μια διαφορετική προσέγγιση από αυτή του Νίκου στην όμορφη πρόταση του Κώστα
 Έστω
Έστω  και ας είναι
και ας είναι  . Τότε προφανώς το τετράπλευρο
. Τότε προφανώς το τετράπλευρο  είναι εγγράψιμο σε κύκλο διαμέτρου
είναι εγγράψιμο σε κύκλο διαμέτρου  (αφού
(αφού  ) και η
) και η  είναι η ευθεία Gauss του πλήρους τετραπλεύρου
είναι η ευθεία Gauss του πλήρους τετραπλεύρου  (με
(με 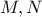 τα μέσα των διαγωνίων του
τα μέσα των διαγωνίων του  ) και συνεπώς
) και συνεπώς  το μέσο της
το μέσο της  (δηλαδή το κέντρου του περιγεγραμμένου κύκλου του τετραπλεύρου
(δηλαδή το κέντρου του περιγεγραμμένου κύκλου του τετραπλεύρου  ). Με τη σειρά
). Με τη σειρά  αρμονική (κάθε διαγώνιος πλήρους τετραπλεύρου τέμνεται αρμονικά από τις άλλες δύο) θα είναι και η δέσμη
αρμονική (κάθε διαγώνιος πλήρους τετραπλεύρου τέμνεται αρμονικά από τις άλλες δύο) θα είναι και η δέσμη  αρμονική και με
αρμονική και με  θα είναι
θα είναι  διχοτόμος της
διχοτόμος της  (συμπληρώματα ίσων γωνιών) και με
(συμπληρώματα ίσων γωνιών) και με




 ομοκυκλικά , άρα
ομοκυκλικά , άρα  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί. προκύπτει συντομότερα από την αρμονική δέσμη
προκύπτει συντομότερα από την αρμονική δέσμη  και ότι
και ότι  το μέσο της
το μέσο της 
Καλησπέρα σε όλους!
 η προβολή του
η προβολή του  στην
στην 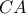 και
και  το συμμετρικό του
το συμμετρικό του  ως προς
ως προς  Τότε το
Τότε το  είναι παραλληλόγραμμο
είναι παραλληλόγραμμο 


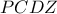 είναι εγγράψιμο,
είναι εγγράψιμο,  άρα η
άρα η  εφάπτεται στον περίκυκλο
εφάπτεται στον περίκυκλο  αλλά και του
αλλά και του  οπότε το
οπότε το  είναι σημείο του κύκλου διαμέτρου
είναι σημείο του κύκλου διαμέτρου  και το ζητούμενο έπεται.
και το ζητούμενο έπεται.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης