 και
και  τα σεβιανά τρίγωνα δύο τυχαίων σημείων
τα σεβιανά τρίγωνα δύο τυχαίων σημείων  στο εσωτερικό τριγώνου
στο εσωτερικό τριγώνου 
και έστω 3 κύκλοι που, έκαστος διέρχεται από τα ζεύγη σημείων

και εφάπτεται στον περίκυκλο του
 , στα σημεία
, στα σημεία  αντίστοιχα.
αντίστοιχα.Δείξτε ότι οι
 συντρέχουν
συντρέχουνΣυντονιστές: vittasko, silouan, rek2
 και
και  τα σεβιανά τρίγωνα δύο τυχαίων σημείων
τα σεβιανά τρίγωνα δύο τυχαίων σημείων  στο εσωτερικό τριγώνου
στο εσωτερικό τριγώνου 

 , στα σημεία
, στα σημεία  αντίστοιχα.
αντίστοιχα. συντρέχουν
συντρέχουνΩραία η άσκηση.



 αρκεί:
αρκεί:
 λαμβάνουμε αντίστοιχα:
λαμβάνουμε αντίστοιχα:



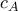 ο κύκλος που εφάπτεται του περίκυκλου στο
ο κύκλος που εφάπτεται του περίκυκλου στο  με ακτίνα
με ακτίνα  και
και  η ακτίνα του περίκυκλου. Έστω
η ακτίνα του περίκυκλου. Έστω  οι τομές των
οι τομές των  με τον
με τον 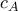 . Εύκολα αποδυκνείεται φέρνοντας την κοινή εφαπτομένη ότι
. Εύκολα αποδυκνείεται φέρνοντας την κοινή εφαπτομένη ότι  .
.


 για να λάβω:
για να λάβω:

 .
.

 η δύναμη του σημείου
η δύναμη του σημείου  ως προς τον κύκλο
ως προς τον κύκλο  .
. 


 για τα
για τα 



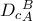 είναι η δύναμη του σημείου
είναι η δύναμη του σημείου  ως προς τον κύκλο
ως προς τον κύκλο 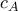 . Ομοίως οι υπόλοιπες.
. Ομοίως οι υπόλοιπες.  βρίσκονται σε κωνική.(Είναι γενίκευση λόγω του θεωρήματος Carnot).
βρίσκονται σε κωνική.(Είναι γενίκευση λόγω του θεωρήματος Carnot).
 οι οποίες θα τέμνουν τις
οι οποίες θα τέμνουν τις 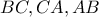 στα
στα  ,θα ισχύει από ομοιότητες πως
,θα ισχύει από ομοιότητες πως  οπότε θα αρκεί τα
οπότε θα αρκεί τα 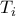 να είναι συνευθειακά.Όμως τα
να είναι συνευθειακά.Όμως τα 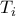 είναι τα κέντρα των αντιστροφών που ανταλλάζουν τα
είναι τα κέντρα των αντιστροφών που ανταλλάζουν τα  κλπ.
κλπ. στην
στην  και παίρνω αντίστοιχο
και παίρνω αντίστοιχο  ώστε τα
ώστε τα 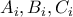 να βρίσκονταισε κωνική (κρατώ σταθερά τα άλλα σημεία),τα
να βρίσκονταισε κωνική (κρατώ σταθερά τα άλλα σημεία),τα  βρίσκονται σε ενέλιξη που ανταλλαζει τα
βρίσκονται σε ενέλιξη που ανταλλαζει τα  (όταν εκφυλιστεί η κωνική).Μια ενέλιξη καθορίζεται από 2 ζεύγη σημείων,άρα η παραπάνω ενέλιξη είναι η αντιστροφή κέντρου
(όταν εκφυλιστεί η κωνική).Μια ενέλιξη καθορίζεται από 2 ζεύγη σημείων,άρα η παραπάνω ενέλιξη είναι η αντιστροφή κέντρου  .Αυτό μου επιτρέπει να κάνω τα
.Αυτό μου επιτρέπει να κάνω τα  να ταυτιστούν στο σταθερό σημείο της ενέλιξης/αντιστροφής,και ομοίως και τα άλλα ζεύγη.Από θ.Brianchon για την εγγεγραμμένη κωνική μετά τις παραπάνω μετακινήσεις,οι
να ταυτιστούν στο σταθερό σημείο της ενέλιξης/αντιστροφής,και ομοίως και τα άλλα ζεύγη.Από θ.Brianchon για την εγγεγραμμένη κωνική μετά τις παραπάνω μετακινήσεις,οι 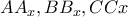 συντρέχουν.Τα T_{i} είναι τα κέντρα των ορθογώνιων κύκλων στον
συντρέχουν.Τα T_{i} είναι τα κέντρα των ορθογώνιων κύκλων στον  που περνούν από τα
που περνούν από τα  και έχουν διαμέτρους στις πλευρές του
και έχουν διαμέτρους στις πλευρές του  (αντίστοιχα).Δεν είναι δύσκολο ότι είναι τα μέσα των διαγωνίων του τετραπλεύρου που δημιουργούνται από τις πλευρές του
(αντίστοιχα).Δεν είναι δύσκολο ότι είναι τα μέσα των διαγωνίων του τετραπλεύρου που δημιουργούνται από τις πλευρές του 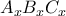 και την τριγραμμική πολική του
και την τριγραμμική πολική του  (τομή
(τομή  ABC$ άρα από Θ. Newton είναι συνευθειακά..
ABC$ άρα από Θ. Newton είναι συνευθειακά.. κωνική τέμνει τις πλευρές του στα
κωνική τέμνει τις πλευρές του στα  .
. τέμνουν τον περίκυκλο του
τέμνουν τον περίκυκλο του  στα
στα  .
. τέμνουν τις
τέμνουν τις 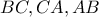 στα
στα  .
. ανήκουν σε κοινή κωνική.
ανήκουν σε κοινή κωνική. είναι σεβιανά 2 σημείων,το
είναι σεβιανά 2 σημείων,το  είναι σεβιανό κάποιου σημείου και ζητάει ν.δ.ο. και το
είναι σεβιανό κάποιου σημείου και ζητάει ν.δ.ο. και το  είναι σεβιανό κάποιου σημείου.(με άλλα λόγια τα 3 σεβιανά δίνουν 4).Είναι απλό πως λόγω μονοσήμαντου,όποια 3 σεβιανά και να επιλέξουμε φτάνουμε σε ισοδύναμο πρόβλημα.Στην παραπάνω γενίκευση,αν έχουμε σεβιανά τα
είναι σεβιανό κάποιου σημείου.(με άλλα λόγια τα 3 σεβιανά δίνουν 4).Είναι απλό πως λόγω μονοσήμαντου,όποια 3 σεβιανά και να επιλέξουμε φτάνουμε σε ισοδύναμο πρόβλημα.Στην παραπάνω γενίκευση,αν έχουμε σεβιανά τα  ,
, (που δεν είναι απαραίτητο) και ένα σεβιανό με κορυφές μεταξύ των
(που δεν είναι απαραίτητο) και ένα σεβιανό με κορυφές μεταξύ των  (που επίσης δεν είναι απαραίτητο),από Θεώρημα
(που επίσης δεν είναι απαραίτητο),από Θεώρημα  και λόγω της κωνικής,θα βγει και το δεύτερο τρίγωνο με κορυφές μεταξύ των
και λόγω της κωνικής,θα βγει και το δεύτερο τρίγωνο με κορυφές μεταξύ των  σεβιανό πράγμα που είναι και το ζητούμενο.Άρα όντως αυτή η γενίκευση είναι γενικότερη..
σεβιανό πράγμα που είναι και το ζητούμενο.Άρα όντως αυτή η γενίκευση είναι γενικότερη.. ταυτίζονται (και τα κυκλικά τους).)
ταυτίζονται (και τα κυκλικά τους).)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες