 και
και  το έκκεντρο και τα παράκεντρά του.
το έκκεντρο και τα παράκεντρά του.Ας είναι
 τα συμμετρικά των παρακέντρων ως προς τις
τα συμμετρικά των παρακέντρων ως προς τις 
Νδο:
1)Οι
 συντρέχουν σε σημείο
συντρέχουν σε σημείο  .
.2)Ισχύει πως
 όπου
όπου  το σημείο
το σημείο  του
του  (το σημείο που ο έγκυκλος εφάπτεται στον κύκλο του
(το σημείο που ο έγκυκλος εφάπτεται στον κύκλο του  του
του  ).
).Συντονιστές: vittasko, silouan, rek2
 και
και  το έκκεντρο και τα παράκεντρά του.
το έκκεντρο και τα παράκεντρά του. τα συμμετρικά των παρακέντρων ως προς τις
τα συμμετρικά των παρακέντρων ως προς τις 
 συντρέχουν σε σημείο
συντρέχουν σε σημείο  .
. όπου
όπου  το σημείο
το σημείο  του
του  (το σημείο που ο έγκυκλος εφάπτεται στον κύκλο του
(το σημείο που ο έγκυκλος εφάπτεται στον κύκλο του  του
του  ).
). και έστω πως εφάπτεται στις
και έστω πως εφάπτεται στις  στα σημεία
στα σημεία  .
. 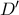 το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το  και
και  το συμμετρικό του
το συμμετρικό του  ως προς το
ως προς το 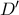 .
. είναι συνευθειακά.
είναι συνευθειακά.  το σημείο επαφής του
το σημείο επαφής του  -παραγεγραμμένου κύκλου με την
-παραγεγραμμένου κύκλου με την  (δηλαδή το σημείο τομής της
(δηλαδή το σημείο τομής της  με την
με την  ).
). και
και  και οι
και οι  και
και  είναι παράλληλες, προκύπτει ότι οι
είναι παράλληλες, προκύπτει ότι οι  ,
,  και
και 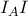 συντρέχουν.
συντρέχουν.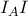 και
και  ως γνωστό διέρχονται από το
ως γνωστό διέρχονται από το  (για την δεύτερη ευθεία είναι γνωστό λήμμα), οπότε τελικά τα
(για την δεύτερη ευθεία είναι γνωστό λήμμα), οπότε τελικά τα  ,
,  ,
, 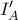 είναι συνευθειακά.
είναι συνευθειακά. και λόγο
και λόγο  . Θεωρούμε τώρα
. Θεωρούμε τώρα  τα μέσα των
τα μέσα των  .
. συντρέχουν στο
συντρέχουν στο 
 .
. διέρχεται από το
διέρχεται από το 
 και όμοια θα ισχύει και για τις άλλες.
και όμοια θα ισχύει και για τις άλλες. . Σε αυτόν ανήκουν τα
. Σε αυτόν ανήκουν τα  και
και  . Έστω πως οι
. Έστω πως οι  και
και  τέμνουν τις
τέμνουν τις  και
και  στα σημεία
στα σημεία  και
και  αντίστοιχα.
αντίστοιχα. και
και  , όπως και
, όπως και 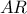 και
και  είναι κάθετες. Οπότε τα
είναι κάθετες. Οπότε τα  και
και  ανήκουν στον κύκλο διαμέτρου
ανήκουν στον κύκλο διαμέτρου  .
. και
και  τα συμμετρικά του
τα συμμετρικά του  ως προς τα
ως προς τα  και
και  αντίστοιχα.
αντίστοιχα. έχουμε πως η
έχουμε πως η  είναι διάμεσος και ύψος, οπότε είναι και διχοτόμος, δηλαδή τελικά το
είναι διάμεσος και ύψος, οπότε είναι και διχοτόμος, δηλαδή τελικά το  ανήκει στην
ανήκει στην  , όπως και το
, όπως και το  .
. και
και  τα μέσα των
τα μέσα των  και
και  . Ισχύει τώρα ότι
. Ισχύει τώρα ότι  και ότι
και ότι  , άρα αφού
, άρα αφού  τα
τα  είναι συνευθειακά.
είναι συνευθειακά. (δηλαδή η
(δηλαδή η  ) τέμνει την
) τέμνει την  στο
στο  και πως η
και πως η  τέμνει τον εγγεγραμμένο κύκλο στο
τέμνει τον εγγεγραμμένο κύκλο στο  .
.  είναι το σημείο
είναι το σημείο  του
του  .
. τέμνει τον κύκλο διαμέτρου
τέμνει τον κύκλο διαμέτρου  στα σημεία
στα σημεία  .
. ως η τομή των
ως η τομή των  και
και  ανήκει στην πολική του
ανήκει στην πολική του  , οπότε τα
, οπότε τα  .
.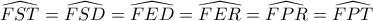 , οπότε το
, οπότε το  είναι εγγράψιμο και συνεπώς
είναι εγγράψιμο και συνεπώς 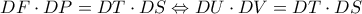 .
. είναι μέσο του
είναι μέσο του  , οπότε λαμβάνοντας υπόψιν ότι το
, οπότε λαμβάνοντας υπόψιν ότι το  είναι το κέντρο του κύκλου διαμέτρου
είναι το κέντρο του κύκλου διαμέτρου  προκύπτει ότι
προκύπτει ότι  , δηλαδή
, δηλαδή  , δηλαδή η
, δηλαδή η  διέρχεται από το αντιδιαμετρικό του
διέρχεται από το αντιδιαμετρικό του  στον εγγεγραμμένο κύκλο, δηλαδή το
στον εγγεγραμμένο κύκλο, δηλαδή το 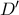 .
. είναι συνευθειακά και το ζητούμενο έπεται!
είναι συνευθειακά και το ζητούμενο έπεται!Καλησπέρα!
 ,
, το ορθικό του και
το ορθικό του και  τα συμμετρικά των
τα συμμετρικά των  ως προς τις
ως προς τις  .Να δειχθεί ότι
.Να δειχθεί ότι 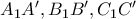 συντρέχουν:
συντρέχουν: .
. όμοια το
όμοια το 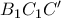 προκύπτει από το
προκύπτει από το 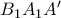 από στροφή κέντρου
από στροφή κέντρου  και γωνίας
και γωνίας  και ομοιοθεσία ( τα παραπάνω χρειάζονται περισσότερη δικαιολόγιση;)
και ομοιοθεσία ( τα παραπάνω χρειάζονται περισσότερη δικαιολόγιση;) είναι
είναι 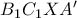 εγγράψιμο .
εγγράψιμο .
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες