 είναι το έγκεντρο και το βαρύκεντρο αντίστοιχα ενός τριγώνου
είναι το έγκεντρο και το βαρύκεντρο αντίστοιχα ενός τριγώνου  Να βρεθεί μία σχέση
Να βρεθεί μία σχέση ανάμεσα στις πλευρές
 αν είναι γνωστό ότι τα σημεία
αν είναι γνωστό ότι τα σημεία  είναι ομοκυκλικά.
είναι ομοκυκλικά.Συντονιστές: vittasko, silouan, rek2
 είναι το έγκεντρο και το βαρύκεντρο αντίστοιχα ενός τριγώνου
είναι το έγκεντρο και το βαρύκεντρο αντίστοιχα ενός τριγώνου  Να βρεθεί μία σχέση
Να βρεθεί μία σχέση  αν είναι γνωστό ότι τα σημεία
αν είναι γνωστό ότι τα σημεία  είναι ομοκυκλικά.
είναι ομοκυκλικά.
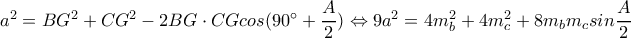 .
.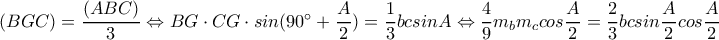
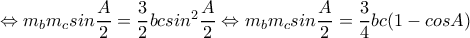

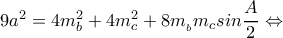

 .
. , ενώ είναι στην πραγματικότητα
, ενώ είναι στην πραγματικότητα .
. παράκεντρο .
παράκεντρο . είναι εγγεγραμμένο σε κύκλο με κέντρο
είναι εγγεγραμμένο σε κύκλο με κέντρο  .
.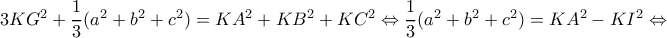
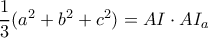
 ομοια και άρα
ομοια και άρα 
 .
.george visvikis έγραψε: ↑Πέμ Φεβ 06, 2020 1:32 pmΣχέση πλευρών...png
είναι το έγκεντρο και το βαρύκεντρο αντίστοιχα ενός τριγώνου
Να βρεθεί μία σχέση
ανάμεσα στις πλευρέςαν είναι γνωστό ότι τα σημεία
είναι ομοκυκλικά.
 το κέντρο του κύκλου
το κέντρο του κύκλου  τότε το
τότε το  ως γνωστών θα είναι το μέσο του τόξου
ως γνωστών θα είναι το μέσο του τόξου  του κύκλου
του κύκλου  που δεν περιέχει το
που δεν περιέχει το  .
. (βαρύκεντρο) ανήκει στον κύκλο.Θεωρώ
(βαρύκεντρο) ανήκει στον κύκλο.Θεωρώ  σημείο στον κύκλο
σημείο στον κύκλο  ώστε
ώστε  .
. το μέσο του τόξου
το μέσο του τόξου  του κύκλου
του κύκλου 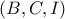 δηλαδή
δηλαδή 
 μεσοκάθετος του
μεσοκάθετος του  και
και  συνευθειακά θα είναι
συνευθειακά θα είναι  και
και  θα είναι το σημείο Lemoine του
θα είναι το σημείο Lemoine του  .
. όπου
όπου  η
η  - συμμετροδιάμεσος πρέπει
- συμμετροδιάμεσος πρέπει 
 (τυχαίο σημείο) ανήκει στον
(τυχαίο σημείο) ανήκει στον  τότε ανήκει και το ισογώνιο συζυγές του.
τότε ανήκει και το ισογώνιο συζυγές του. παράκεντρο και
παράκεντρο και  ο κύκλος
ο κύκλος  .
. τέμνει τον κύκλο ξανά στο
τέμνει τον κύκλο ξανά στο  .
. όμοια και άρα
όμοια και άρα  .
.
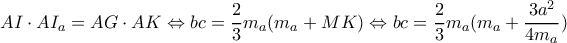
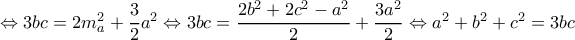

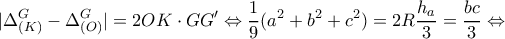

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες