Για τα α) και β) αρκεί να δείξουμε πως ο
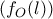
είναι ορθογώνιος στον

...
Θα χρησιμοποιήσουμε την μέθοδο "Deleting Evil Points".
Έστω πως η ευθεία

τέμνει τις

στα

αντίστοιχα. Έστω πως οι συμμετρικές της

ως προς τις

και

τέμνονται στο

, ενώ ομοίως ορίζουμε τα

και

.
Παρατηρούμε πως το

είναι το παράκεντρο του

ως προς την κορυφή

, το

είναι το έγκεντρο του

και το

είναι το είναι το παράκεντρο του

(οι σχέσεις παρακέντρου-εγκέντρου μπορεί να αλλάζουν από σχήμα σε σχήμα, αλλά η ουσία μένει ίδια).
Πρακτικά λοιπόν βλέπουμε πως οι
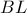
και

είναι διχοτόμοι στο τρίγωνο

. Μπορούμε να θεωρήσουμε

το σημείο τομής τους και με angle chasing προκύπτει πως το

ανήκει στον κύκλο

.
Αν θεωρήσουμε ακόμη

το συμμετρικό του

ως προς την

, βλέπουμε πως αυτό ανήκει στην

.
Μπορούμε ακόμη να ισχυριστούμε πως ο κύκλος

, στην πραγματικότητα είναι ο κύκλος που διέρχεται από τα

ώστε η εγγεγραμμένη γωνία που βαίνει στο τόξο

να ισούται με

(ή την παραπληρωματική της).
Μπορούμε λοιπόν να απλοποιήσουμε το πρόβλημα στο εξής πιο φιλικό και ήμερο (εστιάζοντας στο τρίγωνο

):
---------------------------------------------------------------------------------------------------------------------------
Έστω τρίγωνο

(αυτό είναι το

) με περίκεντρο

και έστω

το συμμετρικό του

ως προς την

. Έστω ακόμη πως μια τυχαία ευθεία που διέρχεται από το

τέμνει τις

και

στα

και

αντίστοιχα. Τότε ο κύκλος που είναι ορθογώνιος στον

και διέρχεται από τα

έχει εγγεγραμμένη γωνία στο τόξο

ίση με

.
Αν θεωρήσουμε τον περιγεγραμμένο κύκλο του

και

το σημείο τομής του με την

, τότε αφού τα

είναι συζυγή σε αντιστροφή κύκλου

, ο ορθογώνιος κύκλος που αναφερόμασταν είναι ο

. Αρκεί λοιπόν να δείξουμε ότι

.
Έστω πως η

τέμνει τον κύκλο

στο

. Εύκολα βλέπουμε πως το

ανήκει στην

. Ακόμη έστω πως η

τέμνει τον κύκλο

στο

.
Βλέπουμε εύκολα πως
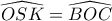
, άρα αρκεί τα

να είναι συνευθειακά.
Αλλάζουμε πάλι λίγο το πρόβλημα σε ισοδύναμο που να μας βολεύει περισσότερο! Θεωρούμε δηλαδή το

ως την τομή της

με την

(με άλλα λόγια την

) και θέλουμε να δείξουμε πως τα
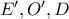
είναι συνευθειακά (ώστε

).
Αυτό όμως προκύπτει με Pascal στο

.
 με
με  το περίκεντρό του.
το περίκεντρό του. μια ευθεία που περνά από το
μια ευθεία που περνά από το  .Ορίζουμε ως
.Ορίζουμε ως 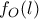 το τρίγωνο που ορίζεται από τις συμμετρικές της
το τρίγωνο που ορίζεται από τις συμμετρικές της  προς τις
προς τις  και ως
και ως  τον περίκυκλο του τριγώνου αυτού.
τον περίκυκλο του τριγώνου αυτού. δεν είναι δυνατόν να εφάπτεται στον
δεν είναι δυνατόν να εφάπτεται στον  .
.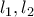 που περνούν από το
που περνούν από το  τέτοιες ώστε οι
τέτοιες ώστε οι  να εφάπτονται.
να εφάπτονται. .
. είναι το μοναδικό σημείο στο εσωτερικό του
είναι το μοναδικό σημείο στο εσωτερικό του  με την τελευταία ιδιότητα.
με την τελευταία ιδιότητα. για τυχαίο σημείο
για τυχαίο σημείο  στο εσωτερικό του
στο εσωτερικό του  /και ευθεία που διέρχεται από αυτό.
/και ευθεία που διέρχεται από αυτό. τέμνονται στα
τέμνονται στα  .
. εφάπτεται σε σταθερή κωνική-καθώς μεταβάλλουμε την
εφάπτεται σε σταθερή κωνική-καθώς μεταβάλλουμε την  .
.
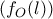 είναι ορθογώνιος στον
είναι ορθογώνιος στον  στα
στα  αντίστοιχα. Έστω πως οι συμμετρικές της
αντίστοιχα. Έστω πως οι συμμετρικές της  και
και  τέμνονται στο
τέμνονται στο  , ενώ ομοίως ορίζουμε τα
, ενώ ομοίως ορίζουμε τα  και
και  .
. ως προς την κορυφή
ως προς την κορυφή  , το
, το  είναι το έγκεντρο του
είναι το έγκεντρο του  και το
και το  είναι το είναι το παράκεντρο του
είναι το είναι το παράκεντρο του  (οι σχέσεις παρακέντρου-εγκέντρου μπορεί να αλλάζουν από σχήμα σε σχήμα, αλλά η ουσία μένει ίδια).
(οι σχέσεις παρακέντρου-εγκέντρου μπορεί να αλλάζουν από σχήμα σε σχήμα, αλλά η ουσία μένει ίδια).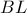 και
και  είναι διχοτόμοι στο τρίγωνο
είναι διχοτόμοι στο τρίγωνο  . Μπορούμε να θεωρήσουμε
. Μπορούμε να θεωρήσουμε  το σημείο τομής τους και με angle chasing προκύπτει πως το
το σημείο τομής τους και με angle chasing προκύπτει πως το  το συμμετρικό του
το συμμετρικό του  , βλέπουμε πως αυτό ανήκει στην
, βλέπουμε πως αυτό ανήκει στην  .
. , στην πραγματικότητα είναι ο κύκλος που διέρχεται από τα
, στην πραγματικότητα είναι ο κύκλος που διέρχεται από τα  ώστε η εγγεγραμμένη γωνία που βαίνει στο τόξο
ώστε η εγγεγραμμένη γωνία που βαίνει στο τόξο  να ισούται με
να ισούται με  (ή την παραπληρωματική της).
(ή την παραπληρωματική της). ):
): και
και  αντίστοιχα. Τότε ο κύκλος που είναι ορθογώνιος στον
αντίστοιχα. Τότε ο κύκλος που είναι ορθογώνιος στον  έχει εγγεγραμμένη γωνία στο τόξο
έχει εγγεγραμμένη γωνία στο τόξο  ίση με
ίση με  και
και  το σημείο τομής του με την
το σημείο τομής του με την  , τότε αφού τα
, τότε αφού τα  είναι συζυγή σε αντιστροφή κύκλου
είναι συζυγή σε αντιστροφή κύκλου  . Αρκεί λοιπόν να δείξουμε ότι
. Αρκεί λοιπόν να δείξουμε ότι  .
.  τέμνει τον κύκλο
τέμνει τον κύκλο  . Εύκολα βλέπουμε πως το
. Εύκολα βλέπουμε πως το  τέμνει τον κύκλο
τέμνει τον κύκλο 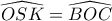 , άρα αρκεί τα
, άρα αρκεί τα  να είναι συνευθειακά.
να είναι συνευθειακά. ως την τομή της
ως την τομή της  με την
με την  ) και θέλουμε να δείξουμε πως τα
) και θέλουμε να δείξουμε πως τα 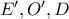 είναι συνευθειακά (ώστε
είναι συνευθειακά (ώστε  ).
). .
.