 ο κύκλος διαμέτρου
ο κύκλος διαμέτρου  εφάπτεται της
εφάπτεται της  Να δείξετε
Να δείξετε ότι και ο κύκλος διαμέτρου
 εφάπτεται της
εφάπτεται της  αν και μόνο αν
αν και μόνο αν 
Συντονιστές: vittasko, silouan, rek2
 ο κύκλος διαμέτρου
ο κύκλος διαμέτρου  εφάπτεται της
εφάπτεται της  Να δείξετε
Να δείξετε  εφάπτεται της
εφάπτεται της  αν και μόνο αν
αν και μόνο αν 
Καλημέρα Γιώργο ,καλημέρα Στάθη και πολύχρονος με καθυστέρηση.......george visvikis έγραψε: ↑Πέμ Σεπ 09, 2021 10:08 amΕφαπτόμενες πλευρές.png
Σε κυρτό τετράπλευροο κύκλος διαμέτρου
εφάπτεται της
Να δείξετε
ότι και ο κύκλος διαμέτρουεφάπτεται της
αν και μόνο αν

 εφάπτεται της
εφάπτεται της  στο σημείο
στο σημείο  και
και 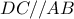 . Εστω
. Εστω  θα αποδειχθεί ότι
θα αποδειχθεί ότι 
 και το τετράπλευρο
και το τετράπλευρο  είναι εγράψιμο σε κύκλο άρα
είναι εγράψιμο σε κύκλο άρα  και τα τετράπλευρα
και τα τετράπλευρα 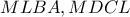 είναι εγράψιμα αφού
είναι εγράψιμα αφού 

 .
.
 εφάπτεται στην
εφάπτεται στην 
 εφάπτεται στη
εφάπτεται στη  και ο κύκλος
και ο κύκλος  εφάπτεται στη
εφάπτεται στη  Θα αποδειχθεί ότι
Θα αποδειχθεί ότι 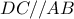

 είναι εγγράψιμο σε κύκλο
είναι εγγράψιμο σε κύκλο 

 είναι εγγράψιμα σε κύκλο .
είναι εγγράψιμα σε κύκλο .




Έστωgeorge visvikis έγραψε: ↑Πέμ Σεπ 09, 2021 10:08 amΕφαπτόμενες πλευρές.png
Σε κυρτό τετράπλευροο κύκλος διαμέτρου
εφάπτεται της
Να δείξετε
ότι και ο κύκλος διαμέτρουεφάπτεται της
αν και μόνο αν

 και ο κύκλος διαμέτρου
και ο κύκλος διαμέτρου  (κέντρου
(κέντρου  (το μέσο της
(το μέσο της  ) εφάπτεται της
) εφάπτεται της  στο σημείο
στο σημείο  (προφανώς
(προφανώς  και
και  ). Αρκεί να δείξουμε ότι
). Αρκεί να δείξουμε ότι  όπου
όπου  η ορθή προβολή του μέσου
η ορθή προβολή του μέσου  της
της  στην
στην  .
. είναι εγγράψιμο σε κύκλο διαμέτρου
είναι εγγράψιμο σε κύκλο διαμέτρου  (λόγω των ορθών γωνιών…) και
(λόγω των ορθών γωνιών…) και  (διάμεσο «τραπεζίου»)
(διάμεσο «τραπεζίου») και συνεπώς τα τετράπλευρα
και συνεπώς τα τετράπλευρα  είναι εγγράψιμα σε κύκλους οπότε:
είναι εγγράψιμα σε κύκλους οπότε: 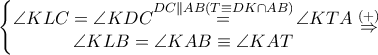
 και συνεπώς και ο κύκλος διαμέτρου
και συνεπώς και ο κύκλος διαμέτρου  εφάπτεται της
εφάπτεται της 
 οι κύκλοι διαμέτρων
οι κύκλοι διαμέτρων  εφάπτονται των
εφάπτονται των  στα σημεία
στα σημεία  αντίστοιχα.. Τότε τα τρίγωνα
αντίστοιχα.. Τότε τα τρίγωνα  είναι ορθογώνια στα
είναι ορθογώνια στα  αντίστοιχα και
αντίστοιχα και  με
με 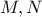 τα μέσα των
τα μέσα των  αντίστοιχα και αρκεί να δειχθεί ότι
αντίστοιχα και αρκεί να δειχθεί ότι 
 είναι εγγράψιμο σε κύκλο διαμέτρου
είναι εγγράψιμο σε κύκλο διαμέτρου  (λόγω των ορθών γωνιών…) και τα τρίγωνα
(λόγω των ορθών γωνιών…) και τα τρίγωνα  είναι ισοσκελή (λόγων των ορθογωνίων τριγώνων και των διαμέσων τους προς την υποτείνουσα)
είναι ισοσκελή (λόγων των ορθογωνίων τριγώνων και των διαμέσων τους προς την υποτείνουσα) εγγράψιμο σε κύκλο και ομοίως και
εγγράψιμο σε κύκλο και ομοίως και  εγγράψιμο σε κύκλο , οπότε
εγγράψιμο σε κύκλο , οπότε  αντιπαράλληλη της
αντιπαράλληλη της  που είναι αντιπαράλληλη της
που είναι αντιπαράλληλη της  , άρα
, άρα  και το αντίστροφο έχει αποδειχθεί.
και το αντίστροφο έχει αποδειχθεί. Ήταν το 4ο πρόβλημα της 25ης Διεθνούς Μαθηματικής Ολυμπιάδας το 1984 που διεξήχθη στην Τσεχοσλαβακία και είχε προταθεί από τον Laurentiu Panaitopol.
Ήταν το 4ο πρόβλημα της 25ης Διεθνούς Μαθηματικής Ολυμπιάδας το 1984 που διεξήχθη στην Τσεχοσλαβακία και είχε προταθεί από τον Laurentiu Panaitopol. Τέθηκε ξανά το 2015 στην Γερμανική Εθνική Ολυμπιάδα (5ο πρόβλημα).
Τέθηκε ξανά το 2015 στην Γερμανική Εθνική Ολυμπιάδα (5ο πρόβλημα). Είδαμε ακόμα το πρώτο σκέλος (Αν το ABCD είναι τραπέζιο) στον δεύτερο γύρο του Εθνικού διαγωνισμού της Πολωνίας το 2018(4ο πρόβλημα).
Είδαμε ακόμα το πρώτο σκέλος (Αν το ABCD είναι τραπέζιο) στον δεύτερο γύρο του Εθνικού διαγωνισμού της Πολωνίας το 2018(4ο πρόβλημα).Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες