Πρόκειται για το θέμα Ο 585 που το πρότεινε ο Marian Ursărescu από τη Ρουμανία.
Η ημερομηνία υποβολής των λύσεων παρήλθε, έτσι μπορώ να το μοιραστώ μαζί σας.
Αποδείξτε ότι σε κάθε τρίγωνο
 ισχύει
ισχύει
Συντονιστές: vittasko, silouan, rek2
 ισχύει
ισχύει





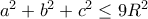

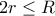

 και ότι
και ότι 
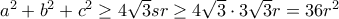

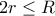
Ωραία λύση κ.ΤηλέμαχεΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Δευ Μάιος 16, 2022 4:51 amΣας παρουσιάζω ένα θέμα από το δεύτερο τεύχος των Mathematical Reflections του 2022.
Πρόκειται για το θέμα Ο 585 που το πρότεινε ο Marian Ursărescu από τη Ρουμανία.
Η ημερομηνία υποβολής των λύσεων παρήλθε, έτσι μπορώ να το μοιραστώ μαζί σας.
Αποδείξτε ότι σε κάθε τρίγωνοισχύει

 η φανταστική μονάδα.
η φανταστική μονάδα. και
και 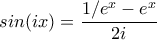 οπότε
οπότε 

 οπότε το παραπάνω γίνεται
οπότε το παραπάνω γίνεται 


 και από την
και από την  η παραπάνω ανάγεται στην
η παραπάνω ανάγεται στην  που ισχύει.
που ισχύει. αν δεν κάνω λάθος)
αν δεν κάνω λάθος)Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες