 , με
, με  το περίκεντρο και το έγκεντρό του αντίστοιχα.
το περίκεντρο και το έγκεντρό του αντίστοιχα.Έστω
 oι ακτίνες των περιγεγραμμένων κύκλων των τριγώνων
oι ακτίνες των περιγεγραμμένων κύκλων των τριγώνων  αντίστοιχα.
αντίστοιχα.Έστω
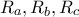 oι ακτίνες των περιγεγραμμένων κύκλων τριγώνων
oι ακτίνες των περιγεγραμμένων κύκλων τριγώνων 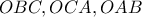 αντίστοιχα.
αντίστοιχα.Αποδείξτε ότι

Συντονιστές: vittasko, silouan, rek2
 , με
, με  το περίκεντρο και το έγκεντρό του αντίστοιχα.
το περίκεντρο και το έγκεντρό του αντίστοιχα. oι ακτίνες των περιγεγραμμένων κύκλων των τριγώνων
oι ακτίνες των περιγεγραμμένων κύκλων των τριγώνων  αντίστοιχα.
αντίστοιχα.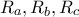 oι ακτίνες των περιγεγραμμένων κύκλων τριγώνων
oι ακτίνες των περιγεγραμμένων κύκλων τριγώνων 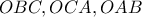 αντίστοιχα.
αντίστοιχα.
Γεια σας,ΚΕΦΑΛΟΝΙΤΗΣ έγραψε: ↑Κυρ Σεπ 25, 2022 6:14 pmΈστω οξυγώνιο τρίγωνο, με
το περίκεντρο και το έγκεντρό του αντίστοιχα.
Έστωoι ακτίνες των περιγεγραμμένων κύκλων των τριγώνων
αντίστοιχα.
Έστωoι ακτίνες των περιγεγραμμένων κύκλων τριγώνων
αντίστοιχα.
Αποδείξτε ότι
 έχουμε
έχουμε 
 έτσι μένει να αποδείξουμε ότι
έτσι μένει να αποδείξουμε ότι 

 όπου
όπου  ισούται με
ισούται με 

 έτσι το
έτσι το ![\sqrt[3]{(2-t)(t+1)^2}\overset {AM-GM}{\leq} \dfrac{2-t+t+1+t+1}{2}=\dfrac{4+t}{3}\leq \dfrac{3}{2} \sqrt[3]{(2-t)(t+1)^2}\overset {AM-GM}{\leq} \dfrac{2-t+t+1+t+1}{2}=\dfrac{4+t}{3}\leq \dfrac{3}{2}](/forum/ext/geomar/texintegr/latexrender/pictures/675b4e733067aef2d30e785224a44e4d.png)
 και η απόδειξη ολοκληρώθηκε.
και η απόδειξη ολοκληρώθηκε.
 έχουμε ότι:
έχουμε ότι:
 .
.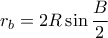 και
και 

 βρίσκουμε ότι:
βρίσκουμε ότι:

 .
. , ότι
, ότι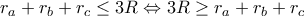
 , τότε έχω την ανισότητα που ήθελα...
, τότε έχω την ανισότητα που ήθελα... , αυτό διαπιστώνεται πολύ εύκολα.
, αυτό διαπιστώνεται πολύ εύκολα.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες