 ,
,  ο περίκυκλός του και
ο περίκυκλός του και  ο έγκυκλός του.
ο έγκυκλός του.Ας είναι επίσης
 το σημείο επαφής του έγκυκλου με την
το σημείο επαφής του έγκυκλου με την  και
και  τα μέσα των
τα μέσα των  αντίστοιχα.
αντίστοιχα.Αν
 , δείξτε ότι ο κύκλος
, δείξτε ότι ο κύκλος  εφάπτεται του περίκυκλου
εφάπτεται του περίκυκλου 
Συντονιστές: vittasko, silouan, rek2
 ,
,  ο περίκυκλός του και
ο περίκυκλός του και  ο έγκυκλός του.
ο έγκυκλός του. το σημείο επαφής του έγκυκλου με την
το σημείο επαφής του έγκυκλου με την  και
και  τα μέσα των
τα μέσα των  αντίστοιχα.
αντίστοιχα. , δείξτε ότι ο κύκλος
, δείξτε ότι ο κύκλος  εφάπτεται του περίκυκλου
εφάπτεται του περίκυκλου 
 τέμνει για δεύτερη φορά τον κύκλο
τέμνει για δεύτερη φορά τον κύκλο  στο σημείο
στο σημείο  .
. .
. εφάπτεται της χορδής
εφάπτεται της χορδής  του κύκλου
του κύκλου  στο σημείο
στο σημείο  ,
, . Θεωρούμε τον κύκλο
. Θεωρούμε τον κύκλο  . Το κέντρο αυτού
. Το κέντρο αυτού  του τόξου
του τόξου  του περιγεγραμμένου κύκλου του
του περιγεγραμμένου κύκλου του 
 (Είναι
(Είναι  , θεώρημα τρίαινας,
, θεώρημα τρίαινας,  το
το 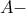 παράκεντρο του τριγώνου
παράκεντρο του τριγώνου  ).
).  και
και  είναι ορθογώνιοι.
είναι ορθογώνιοι. είναι αρμονική, όπου
είναι αρμονική, όπου  το δεύτερο
το δεύτερο  με τον κύκλο
με τον κύκλο  .
. είναι αρμονική, όπου
είναι αρμονική, όπου  .
.  (
( ) τότε και η διαίρεση
) τότε και η διαίρεση  είναι αρμονική, οπότε οι κύκλοι
είναι αρμονική, οπότε οι κύκλοι 
 είναι ορθογώνιοι.
είναι ορθογώνιοι. (εδώ ο
(εδώ ο  ) εφάπτεται της χορδής
) εφάπτεται της χορδής 
 (εδώ ο
(εδώ ο  ) στο σημείο
) στο σημείο  , και επίσης ο κύκλος
, και επίσης ο κύκλος  είναι ορθογώνιος προς έναν κύκλο
είναι ορθογώνιος προς έναν κύκλο 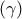
 ).
).  εφάπτεται του κύκλου
εφάπτεται του κύκλου  .
. εφάπτεται χορδής
εφάπτεται χορδής  κύκλου
κύκλου  στο σημείο
στο σημείο  , και του κύκλου
, και του κύκλου  στο σημείο
στο σημείο  .
.  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  .
. το δεύτερο σημείο τομής της
το δεύτερο σημείο τομής της  με τον κύκλο
με τον κύκλο  , και έστω
, και έστω 
 , που τέμνει την ευθεία
, που τέμνει την ευθεία  στο σημείο
στο σημείο  .
.  (γωνία από χορδή και εφαπτομένη). Έστω, επίσης
(γωνία από χορδή και εφαπτομένη). Έστω, επίσης  και
και  .
.  , και εφόσον το τρίγωνο
, και εφόσον το τρίγωνο  είναι ισοσκελές, τότε
είναι ισοσκελές, τότε  ,
,  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  .
. με την οποία ο κύκλος
με την οποία ο κύκλος  μετασχηματίζεται στον κύκλο
μετασχηματίζεται στον κύκλο  .
.  του κύκλου
του κύκλου  μετασχηματίζεται στην εφαπτομένη
μετασχηματίζεται στην εφαπτομένη  στο σημείο
στο σημείο  .
.  , προκύπτει ότι τοξ
, προκύπτει ότι τοξ = τοξ
= τοξ
 , δηλαδή, η
, δηλαδή, η  είναι διχοτόμος της γωνίας
είναι διχοτόμος της γωνίας  .
. .
. και
και  :
:  .)
.)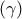 κέντρου
κέντρου  και ακτίνας
και ακτίνας  είναι ορθογώνιος του κύκλου
είναι ορθογώνιος του κύκλου  .
. το ένα από τα δύο κοινά σημεία των κύκλων
το ένα από τα δύο κοινά σημεία των κύκλων  και
και 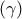 . Από το προηγούμενο είναι
. Από το προηγούμενο είναι  ,
,  (ακτίνες του κύκλου
(ακτίνες του κύκλου 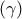 ), τότε
), τότε  , οπότε η ακτίνα
, οπότε η ακτίνα  του κύκλου
του κύκλου 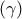 είναι εφαπτομένη
είναι εφαπτομένη  , και επομένως, οι δύο κύκλοι είναι ορθογώνιοι.)
, και επομένως, οι δύο κύκλοι είναι ορθογώνιοι.) και
και  τέμνονται στα σημεία
τέμνονται στα σημεία  και
και  . Ένας τρίτος κύκλος
. Ένας τρίτος κύκλος  με κέντρο επί της ευθείας
με κέντρο επί της ευθείας  είναι ορθογώνιος του κύκλου
είναι ορθογώνιος του κύκλου  . Τότε,ο κύκλος
. Τότε,ο κύκλος  είναι ορθογώνιος και του κύκλου
είναι ορθογώνιος και του κύκλου  .
. και
και  είναι ορθογώνιοι, τότε
είναι ορθογώνιοι, τότε  , όπου
, όπου  το κέντρο του κύκλου
το κέντρο του κύκλου  ,
,  σημείο τομής των κύκλων
σημείο τομής των κύκλων  και
και  . Από το ορθογώνιο τρίγωνο
. Από το ορθογώνιο τρίγωνο  προκύπτει ότι
προκύπτει ότι  .
Έχουμε επίσης ότι
.
Έχουμε επίσης ότι  .
. (ακτίνες του κύκλου
(ακτίνες του κύκλου  ). Ως εκ τούτου,
). Ως εκ τούτου,  ,
, είναι ορθογώνιο, από το οποίο προκύπτει ότι
είναι ορθογώνιο, από το οποίο προκύπτει ότι  , δηλαδή, οι κύκλοι
, δηλαδή, οι κύκλοι  και
και  είναι ορθογώνιοι.
είναι ορθογώνιοι.  είναι ορθογώνιος σε καθένα από δύο τεμνόμενους (στα σημεία
είναι ορθογώνιος σε καθένα από δύο τεμνόμενους (στα σημεία  και
και  ) κύκλους
) κύκλους  και
και  , τότε το κέντρο
, τότε το κέντρο  ανήκει στην ευθεία
ανήκει στην ευθεία  .
. δεν εφάπτεται του κύκλου
δεν εφάπτεται του κύκλου  .
.  , ο οποίος εφάπτεται του κύκλου
, ο οποίος εφάπτεται του κύκλου  , και εφάπτεται επίσης της χορδής
, και εφάπτεται επίσης της χορδής  στο σημείο
στο σημείο 
 και λόγου
και λόγου  , του κύκλου
, του κύκλου  ,
, το μέσο του τόξου
το μέσο του τόξου  του κύκλου
του κύκλου  , και
, και  η τομή
η τομή  ).
Επομένως, το
).
Επομένως, το  είναι το σημείο επαφής των κύκλων
είναι το σημείο επαφής των κύκλων  και
και  , και
, και  είναι το δεύτερο σημείο
είναι το δεύτερο σημείο  και
και  .
.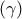 είναι ορθογώνιος του
είναι ορθογώνιος του  (βλέπε παραπάνω). Αφετέρου, από
(βλέπε παραπάνω). Αφετέρου, από  και
και 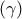 είναι επίσης ορθογώνιοι. Έχουμε λοιπόν ότι ο κύκλος
είναι επίσης ορθογώνιοι. Έχουμε λοιπόν ότι ο κύκλος 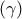
 και
και  . Επομένως, σύμφωνα με προηγούμενη σημείωση το κέντρο του
. Επομένως, σύμφωνα με προηγούμενη σημείωση το κέντρο του 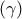 (το σημείο
(το σημείο  ) πρέπει να ανήκει στην ευθεία
) πρέπει να ανήκει στην ευθεία  . Αλλά από το λήμμα Αρχιμήδη
. Αλλά από το λήμμα Αρχιμήδη  ανήκει στην ευθεία
ανήκει στην ευθεία 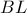 . Επομένως, τα σημεία
. Επομένως, τα σημεία  και
και  συμπίπτουν, από το οποίο
συμπίπτουν, από το οποίοΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης