 το μέσο ημικυκλίου διαμέτρου
το μέσο ημικυκλίου διαμέτρου 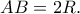 Σε σημείο
Σε σημείο  του τόξου
του τόξου  φέρνω εφαπτομένη
φέρνω εφαπτομένη  του
τουημικυκλίου. Να βρείτε σημείο
 της διαμέτρου
της διαμέτρου  ώστε αν
ώστε αν  είναι οι προβολές των
είναι οι προβολές των 
αντίστοιχα στην
 να ισχύει
να ισχύει 
Συντονιστές: vittasko, silouan, rek2
 το μέσο ημικυκλίου διαμέτρου
το μέσο ημικυκλίου διαμέτρου 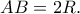 Σε σημείο
Σε σημείο  του τόξου
του τόξου  φέρνω εφαπτομένη
φέρνω εφαπτομένη  του
του της διαμέτρου
της διαμέτρου  ώστε αν
ώστε αν  είναι οι προβολές των
είναι οι προβολές των 
 να ισχύει
να ισχύει 
Νομίζω ότι τα δεδομένα του προβλήματος παραπέμπουν σε αναλυτική γεωμετρία (τις σχέσεις (απλές) της αναλυτικής γεωμετρίας που χρησιμοποιήθηκε μπορείτε να τις μετατρέψετε σε ευκλείδειες σχέσειςgeorge visvikis έγραψε: ↑Κυρ Νοέμ 30, 2025 10:19 amΖητείται θέση.png
Έστωτο μέσο ημικυκλίου διαμέτρου
Σε σημείο
του τόξου
φέρνω εφαπτομένη
του ημικυκλίου. Να βρείτε σημείο
της διαμέτρου
ώστε αν
είναι οι προβολές των
αντίστοιχα στην
να ισχύει

 οπότε αν
οπότε αν  και φυσικά ως προς το εν λόγω σύστημα θα είναι
και φυσικά ως προς το εν λόγω σύστημα θα είναι  και ας είναι
και ας είναι  .
. και
και ,
,  και
και 



Μέλη σε αυτήν τη Δ. Συζήτηση: duamba και 1 επισκέπτης