 της μορφής
της μορφής  , ισχύει ότι
, ισχύει ότι 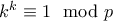
Συντονιστές: cretanman, silouan, rek2
 .
.  είναι τετραγωνικό υπόλοιπο. Έστω
είναι τετραγωνικό υπόλοιπο. Έστω  . Το
. Το  είναι τετραγωνικό υπόλοιπο αν και μόνο αν ο
είναι τετραγωνικό υπόλοιπο αν και μόνο αν ο  είναι της μορφής
είναι της μορφής  και επίσης το
και επίσης το  είναι διτετραγωνικό υπόλοιπο στην ίδια περίπτωση. Άρα το
είναι διτετραγωνικό υπόλοιπο στην ίδια περίπτωση. Άρα το  είναι τετραγωνικό υπόλοιπο και
είναι τετραγωνικό υπόλοιπο και  .
. , ισχύει η ισοδυναμία:
, ισχύει η ισοδυναμία:
 ή ισοδύναμα:
ή ισοδύναμα: 

 , όπου
, όπου  είναι περιττός, άρα έχουμε πως:
είναι περιττός, άρα έχουμε πως: 
 πρώτος της μορφής
πρώτος της μορφής  , ισχύει ότι:
, ισχύει ότι:
Προσοχή, οΔιονύσιος Αδαμόπουλος έγραψε: Τότε.
...
Τότε προφανώς δεν ισχύει ότι, άρα
.
 δεν είναι απαραίτητα πρώτος.
δεν είναι απαραίτητα πρώτος.Νομίζω πως τώρα είναι εντάξει.dement έγραψε:Προσοχή, οΔιονύσιος Αδαμόπουλος έγραψε: Τότε.
...
Τότε προφανώς δεν ισχύει ότι, άρα
.
δεν είναι απαραίτητα πρώτος.
 υπόλοιπα:
υπόλοιπα:


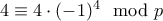
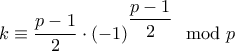
 αν
αν  ή
ή 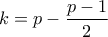 αν
αν 






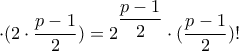


 , άρα προκύπτει ότι:
, άρα προκύπτει ότι:
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες