Να βρεθούν όλα τα ζευγάρια πρώτων
 έτσι ώστε
έτσι ώστε  .
.Συντονιστές: cretanman, silouan, rek2
Μη αναγνωσμένη δημοσίευση από Διονύσιος Αδαμόπουλος » Τρί Φεβ 20, 2018 10:36 pm
 έτσι ώστε
έτσι ώστε  .
.Μη αναγνωσμένη δημοσίευση από min## » Τετ Φεβ 21, 2018 8:25 pm

 ,δηλαδή, από FLT-Euler:
,δηλαδή, από FLT-Euler:
 ,
, και
και  .
. ,
, και η αρχική γίνεται
και η αρχική γίνεται  ,από όπου, με
,από όπου, με  ,παίρνουμε την
,παίρνουμε την  .
.
 διαιρούν τα
διαιρούν τα  ,χωρίς να διαιρούν τα
,χωρίς να διαιρούν τα 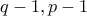 (αντίστοιχα).Όμως,
(αντίστοιχα).Όμως,  ,και αν
,και αν  ,από τα παραπάνω
,από τα παραπάνω  και ομοίως
και ομοίως  άτοπο.
άτοπο. ,
,  για
για  σχετικά πρώτο με το 5, ενώ αν
σχετικά πρώτο με το 5, ενώ αν  ,δεκτό.Από το τελευταίο έπονται οι λύσεις
,δεκτό.Από το τελευταίο έπονται οι λύσεις  .Συνεπώς, συνολικά έχουμε τις
.Συνεπώς, συνολικά έχουμε τις  και τις ανάποδες...
και τις ανάποδες...Επιστροφή σε “Θεωρία Αριθμών - Επίπεδο Αρχιμήδη (Seniors)”
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες
Powered by phpBB® Forum Software © phpBB Limited
Style από Arty - Ενημέρωση phpBB 3.2 από MrGaby
Ελληνική μετάφραση από το phpbbgr.com
Το www.mathematica.gr δημιουργήθηκε από τους Γρηγόρη Κωστάκο και Αλέξανδρο Συγκελάκη
με τη βοήθεια των Στέλιου Μόσχογλου και Γιώργου Μαργαρίτη
GZIP: Off