Διαιρετότητα για θετικούς ακεραίους

panagiotis iliopoulos · #1

Να βρεθούν οι θετικοί ακέραιοι m,n

για τους οποίους ο αριθμός $\frac{n^{3}+1}{mn-1}$ είναι ακέραιος.

#2

Παναγιώτη καλησπέρα. Καλό θα είναι να βάζεις τις ασκήσεις στο φάκελο που ανήκουν (πχ, Αρχιμήδης Senior για την συγκεκριμένη) και όχι στο φάκελο "Γενικά Μηνύματα". Επίσης καλό θα ήταν να γίνεται μια καλύτερη επιλογή στον τίτλο και τις λέξεις κλειδιά ώστε να είναι εύκολη η αναζήτηση στο μέλλον.

#3

Έκανα την μετακίνηση.

Διονύσιος Αδαμόπουλος · #4

Θα είναι και ο αριθμός $\dfrac{n^3+1}{mn-1}+1$ ακέραιος, δηλαδή ο $\dfrac{n(n^2+m)}{mn-1}$ . Είναι (n, mn-1)=1

, επομένως πρέπει και ο αριθμός $\dfrac{n^2+m}{mn-1}$ να είναι ακέραιος.

Έστω $\dfrac{n^2+m}{mn-1}=k$ .

Τότε n^2-kmn+k+m=0

(1) και ισχύει ότι k, m, n

είναι θετικοί ακέραιοι. Η διακρίνουσα είναι D=k^2m^2-4(k+m)

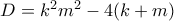και πρέπει να είναι τέλειο τετράγωνο.

Έστω $k\leq m$ .

Αν k=1

τότε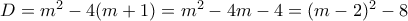

, άρα αφού το

πρέπει να είναι τέλειο τετράγωνο παίρνουμε $(m-2)^2-l^2=8\Leftrightarrow (m-2-l)(m-2+l)=8$ και αφού οι αριθμοί m-2-l

και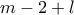

είναι ισοϋπόλοιποι με το

ισχύει ότι m-2-l=2

και

, δηλαδή

.

Αν

τότε

, άρα αφού το

πρέπει να είναι τέλειο τετράγωνο παίρνουμε $(2m-1)^2-l^2=9\Leftrightarrow (2m-1-l)(2m-1+l)=9$ άρα 2m-1-l=1

και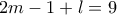

, όπου

, ή

και

, δηλαδή

.

Αν τώρα $k, m\geq 3$ έχουμε πως $(km-2)^2<D\Leftrightarrow 4(k+m)+4<4km\Leftrightarrow k+m+1<km\Leftrightarrow (k-1)(m-1)>2$ που ισχύει.

Όμως ταυτόχρονα είναι D<(km)^2

, επομένως πρέπει $D=(km-1)^2\Leftrightarrow 4(k+m)+1=2km$ , άτοπο αφού το αριστερό μέλος είναι περιττό ενώ το δεξί άρτιο.

Άρα για να έχει η (1) ακέραιες λύσεις ως προς

πρέπει

.

Αντικαθιστώντας στην (1) και διακρίνοντας τις περιπτώσεις παίρνουμε τα αντίστοιχα ζευγάρια (n, m)=(2, 5), (3, 5), (2, 1), (3, 1), (1, 3), (5, 3), (1, 2), (5, 2), (2, 2)

.

Edit: Προσθήκη μιας τετριμμένης περίπτωσης

Ορέστης Λιγνός · #5

Ο δολοφόνος επιστρέφει πάντα στον τόπο του εγκλήματος ! εδώ

Γεια σου Διονύση!

Διονύσιος Αδαμόπουλος · #6

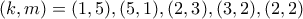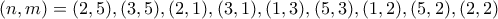Ορέστης Λιγνός έγραψε: ↑
Τετ Μαρ 21, 2018 11:08 pm
Ο δολοφόνος επιστρέφει πάντα στον τόπο του εγκλήματος ! εδώ

Γεια σου Διονύση!

Γεια σου Ορέστη!

Ούτε που τη θυμόμουνα. Ευτυχώς η νέα λύση είναι λίγο διαφορετική από την προηγούμενη!!

#7

panagiotis iliopoulos έγραψε: ↑
Τετ Μαρ 21, 2018 5:44 pm
Να βρεθούν οι θετικοί ακέραιοι για τους οποίους ο αριθμός $\frac{n^{3}+1}{mn-1}$ είναι ακέραιος.

Πρόκειται για το Πρόβλημα 4 της Δ.Μ.Ο του 1994.

Φιλικά,

Αχιλλέας

Διαιρετότητα για θετικούς ακεραίους

Διαιρετότητα για θετικούς ακεραίους

Re: Άσκηση

Re: Άσκηση

Re: Διαιρετότητα για θετικούς ακεραίους

Re: Διαιρετότητα για θετικούς ακεραίους

Re: Διαιρετότητα για θετικούς ακεραίους

Re: Διαιρετότητα για θετικούς ακεραίους

Μέλη σε σύνδεση