
ώστε
 να διαιρείται με δυο το πολύ διαφορετικούς μεταξύ τους πρώτους
να διαιρείται με δυο το πολύ διαφορετικούς μεταξύ τους πρώτουςΣυντονιστές: cretanman, silouan, rek2

 να διαιρείται με δυο το πολύ διαφορετικούς μεταξύ τους πρώτους
να διαιρείται με δυο το πολύ διαφορετικούς μεταξύ τους πρώτουςΚαλησπέρα!
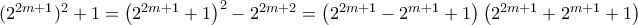
 πρέπει
πρέπει  το οποίο επαληθεύει την συνθήκη.
το οποίο επαληθεύει την συνθήκη.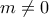
 άρτιος,έστω
άρτιος,έστω 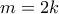
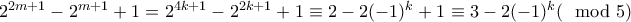

 άρτιος ή περιττός ένας από τους παράγοντες είναι πολλαπλάσιο του
άρτιος ή περιττός ένας από τους παράγοντες είναι πολλαπλάσιο του 
 άτοπο!
άτοπο! ,αυτή τη λύση την έχουμε αναφέρει πιο πάνω.
,αυτή τη λύση την έχουμε αναφέρει πιο πάνω. περιττός,έστω
περιττός,έστω 


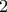 παράγοντες είναι ίσος με πέντε.
παράγοντες είναι ίσος με πέντε.
 ,πάλι
,πάλι 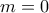
 βλέπουμε πως
βλέπουμε πως  άρα αποτελεί λύση.
άρα αποτελεί λύση.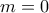 ή
ή 
Λέγοντας με 2 το πολύ διαφορετικούς πρώτους εννοούμε και τις δυνάμεις αυτών;
 έχουμε
έχουμε  που αυτός διαιρείται με δύο το πολύ διαφορετικούς μεταξύ τους πρώτους και ο ένας εξ αυτών ταυτίζεται με άλλον.
που αυτός διαιρείται με δύο το πολύ διαφορετικούς μεταξύ τους πρώτους και ο ένας εξ αυτών ταυτίζεται με άλλον.Οι πρώτοι αυτοί δεν είναι υψωμένοι σε δυνάμειςmiltosk έγραψε: ↑Δευ Αύγ 26, 2019 5:44 pmΛέγοντας με 2 το πολύ διαφορετικούς πρώτους εννοούμε και τις δυνάμεις αυτών;
Για παράδειγμα: γιαέχουμε
που αυτός διαιρείται με δύο το πολύ διαφορετικούς μεταξύ τους πρώτους και ο ένας εξ αυτών ταυτίζεται με άλλον.
Αν δεν εννοείς αυτό όμως νομίζω πως είναι ενδιαφέρουσα τροποποίηση.
petrosqw έγραψε: ↑Δευ Αύγ 26, 2019 6:20 pmΟι πρώτοι αυτοί δεν είναι υψωμένοι σε δυνάμειςmiltosk έγραψε: ↑Δευ Αύγ 26, 2019 5:44 pmΛέγοντας με 2 το πολύ διαφορετικούς πρώτους εννοούμε και τις δυνάμεις αυτών;
Για παράδειγμα: γιαέχουμε
που αυτός διαιρείται με δύο το πολύ διαφορετικούς μεταξύ τους πρώτους και ο ένας εξ αυτών ταυτίζεται με άλλον.
Αν δεν εννοείς αυτό όμως νομίζω πως είναι ενδιαφέρουσα τροποποίηση.
 με
με  . Ουσιαστικά από την εκφώνηση προκύπτει αυτό που λέει ο miltosk. (δεν βάζω πως λύνεται γιατί δεν επιτρέπεται απλή αναφορά)
. Ουσιαστικά από την εκφώνηση προκύπτει αυτό που λέει ο miltosk. (δεν βάζω πως λύνεται γιατί δεν επιτρέπεται απλή αναφορά) είναι
είναι 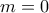 ή
ή  ή
ή 

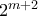
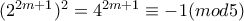
 ,όπου
,όπου  ή
ή 
 ικανοποιείται το ζητούμενο
ικανοποιείται το ζητούμενο 
 είναι άρτιος ,
είναι άρτιος , 


 για κάποιον περιττό
για κάποιον περιττό 
 τοτε:
τοτε: ,άτοπο
,άτοπο 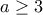 τοτε:
τοτε:
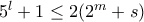 ,άτοπο
,άτοποΜέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες