 για τούς οποίους ο
για τούς οποίους ο είναι τέλειο τετράγωνο
είναι τέλειο τετράγωνο(Δεν έχω λύση.Πιστευω πώς χρειάζεται αλγεβρική θεωρία αριθμών)
Συντονιστές: cretanman, silouan, rek2
 για τούς οποίους ο
για τούς οποίους ο είναι τέλειο τετράγωνο
είναι τέλειο τετράγωνο . Απ' αυτή παίρνουμε πως:
. Απ' αυτή παίρνουμε πως:  . Συνεπώς, πρέπει:
. Συνεπώς, πρέπει:  . Μπορούμε, λοιπόν, να θέσουμε:
. Μπορούμε, λοιπόν, να θέσουμε:  . Αντικαθιστώντας στην αρχική, έχουμε:
. Αντικαθιστώντας στην αρχική, έχουμε:  . Τώρα, διακρίνουμε περιπτώσεις.
. Τώρα, διακρίνουμε περιπτώσεις.  . Τότε, προκειμένου να ισχύει η
. Τότε, προκειμένου να ισχύει η  , προκύπτει η τιμή
, προκύπτει η τιμή  , η οποία δίνει
, η οποία δίνει  και τελικά
και τελικά  . Συνεπώς, η πρώτη τιμή του
. Συνεπώς, η πρώτη τιμή του  είναι η
είναι η  , από την οποία προκύπτει το τέλειο τετράγωνο
, από την οποία προκύπτει το τέλειο τετράγωνο 
 . Θα αποδείξουμε ότι δεν δύνανται να προκύψει τέλειο τετράγωνο, αν
. Θα αποδείξουμε ότι δεν δύνανται να προκύψει τέλειο τετράγωνο, αν  . Έστω προς άτοπο
. Έστω προς άτοπο  . Αντικαθιστώντας στην
. Αντικαθιστώντας στην  , παίρνουμε:
, παίρνουμε:  . Θα αποδείξουμε πως ισχύει:
. Θα αποδείξουμε πως ισχύει:  . Αν δεν ισχύει, με
. Αν δεν ισχύει, με  παίρνουμε πως:
παίρνουμε πως:  . Σύμφωνα με τις σχέσεις που έχουμε θέσει, θα ισχύει:
. Σύμφωνα με τις σχέσεις που έχουμε θέσει, θα ισχύει:  . Οπότε, αντιλαμβανόμαστε πως ισχύει;
. Οπότε, αντιλαμβανόμαστε πως ισχύει;  , ή
, ή 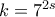 . Τώρα, θα αντικαταστήσουμε την τιμή του
. Τώρα, θα αντικαταστήσουμε την τιμή του  στη σχέση:
στη σχέση:  , παίρνουμε:
, παίρνουμε:  , το οποίο θα αποδείξουμε πως δεν είναι τέλειο τετράγωνο. Έστω
, το οποίο θα αποδείξουμε πως δεν είναι τέλειο τετράγωνο. Έστω  Αντικαθιστώντας στη σχέση που μόλις βρήκαμε, προκύπτει η διοφαντική εξίσωση:
Αντικαθιστώντας στη σχέση που μόλις βρήκαμε, προκύπτει η διοφαντική εξίσωση:  , όπου πρέπει να ισχύει:
, όπου πρέπει να ισχύει:  , που δίνει
, που δίνει  ρητό, πράγμα που απορρίπτεται. Η δεύτερη περίπτωση δίνει πάλι
ρητό, πράγμα που απορρίπτεται. Η δεύτερη περίπτωση δίνει πάλι  ρητό και, συνεπώς, απορρίπτεται επίσης (παρόμοια αποδεικνύεται πως δεν υπάρχουν ακέριες τιμές του
ρητό και, συνεπώς, απορρίπτεται επίσης (παρόμοια αποδεικνύεται πως δεν υπάρχουν ακέριες τιμές του  για
για 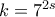 . Συμπερασματικά, ισχύει η ανισότητα
. Συμπερασματικά, ισχύει η ανισότητα  . Για
. Για  προκύπτει
προκύπτει 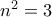 , άτοπο, αφού δεν είναι τέλειο τετράγωνο. Οπότε, όπως έχει προαναφερθεί, η μόνη αποδεκτή τιμή του
, άτοπο, αφού δεν είναι τέλειο τετράγωνο. Οπότε, όπως έχει προαναφερθεί, η μόνη αποδεκτή τιμή του  είναι η
είναι η  , για την οποία προκύπτει η αποδεκτή τιμή
, για την οποία προκύπτει η αποδεκτή τιμή  , που είναι και η μόνη.
, που είναι και η μόνη.Philip.kal έγραψε: ↑Τετ Ιαν 27, 2021 2:01 pmΤώρα, θα αντικαταστήσουμε την τιμή τουστη σχέση:
, παίρνουμε:
, το οποίο σίγουρα δεν είναι τέλειο τετράγωνο, αφού υπάρχουν δύο τετράγωνα φυσικών, όμως ένας από τους όρους δεν είναι τέλειο τετράγωνο, με αποτέλεσμα να μην συμπληρώνεται η πυθαγόρεια τριάδα (
.
 ; Βέβαια διορθώνεται εύκολα...
; Βέβαια διορθώνεται εύκολα...Ευχαριστώ πολύ για την επισήμανση! Έκανα κάποιες διορθώσεις.Τσιαλας Νικολαος έγραψε: ↑Τετ Ιαν 27, 2021 2:09 pmPhilip.kal έγραψε: ↑Τετ Ιαν 27, 2021 2:01 pmΤώρα, θα αντικαταστήσουμε την τιμή τουστη σχέση:
, παίρνουμε:
, το οποίο σίγουρα δεν είναι τέλειο τετράγωνο, αφού υπάρχουν δύο τετράγωνα φυσικών, όμως ένας από τους όρους δεν είναι τέλειο τετράγωνο, με αποτέλεσμα να μην συμπληρώνεται η πυθαγόρεια τριάδα (
.
; Βέβαια διορθώνεται εύκολα...
 .Και υπάρχει πολύ ποίο εύκολη απόδειξη.
.Και υπάρχει πολύ ποίο εύκολη απόδειξη. και έχεις
και έχεις  αλλά το
αλλά το  δεν είναι τετραγωνικό υπόλοιπο
δεν είναι τετραγωνικό υπόλοιπο 
 είναι περιττός. Οπότε ψάχνουμε λύσεις της
είναι περιττός. Οπότε ψάχνουμε λύσεις της
 πρέπει να είναι δύναμη του
πρέπει να είναι δύναμη του  .
. είναι η
είναι η  . Κάθε θεμελιώδης λύση της
. Κάθε θεμελιώδης λύση της  είναι της μορφής
είναι της μορφής  με
με  . Πρέπει επίσης
. Πρέπει επίσης  άρα χρειάζεται να ελέγξουμε μόνο την περίπτωση
άρα χρειάζεται να ελέγξουμε μόνο την περίπτωση  και παίρνουμε τις θεμελιώδεις λύσεις
και παίρνουμε τις θεμελιώδεις λύσεις  και
και  .
. . Όπως και στην περίπτωση της Pell οι υπόλοιπες λύσεις δίνονται από τις αναδρομικές σχέσεις
. Όπως και στην περίπτωση της Pell οι υπόλοιπες λύσεις δίνονται από τις αναδρομικές σχέσεις  και
και  . (
. ( όπου το
όπου το  προκύπτει από τη θεμελιώδη λύση της
προκύπτει από τη θεμελιώδη λύση της  .) Μας ενδιαφέρει η ακολουθία
.) Μας ενδιαφέρει η ακολουθία  αλλά θέλουμε και το
αλλά θέλουμε και το 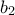 για να συνεχίσουμε. Αυτό δίνεται από τον τύπο
για να συνεχίσουμε. Αυτό δίνεται από τον τύπο  .
.  modulo 7. Είναι η
modulo 7. Είναι η  και μετά επαναλαμβάνεται. Δηλαδή
και μετά επαναλαμβάνεται. Δηλαδή  αν και μόνο αν
αν και μόνο αν  . Βρίσκουμε επίσης ότι
. Βρίσκουμε επίσης ότι  . Τώρα θα κοιτάξω την ακολουθία
. Τώρα θα κοιτάξω την ακολουθία  modulo
modulo  . Θα βρω ότι είναι η
. Θα βρω ότι είναι η  και μετά επαναλαμβάνεται.
και μετά επαναλαμβάνεται. . Άρα δεν υπάρχει
. Άρα δεν υπάρχει  ώστε το
ώστε το  να είναι τέλεια δύναμη του
να είναι τέλεια δύναμη του  εκτός ίσως αν
εκτός ίσως αν  , το οποίο δίνει τη λύση
, το οποίο δίνει τη λύση  .
. . Ευτυχώς
. Ευτυχώς  , μετά
, μετά  και συνεχίζει όπως την προηγούμενη ακολουθία. Άρα δεν προκύπτει οποιαδήποτε καινούργια λύση.
και συνεχίζει όπως την προηγούμενη ακολουθία. Άρα δεν προκύπτει οποιαδήποτε καινούργια λύση. είναι το
είναι το  τέλειο τετράγωνο.
τέλειο τετράγωνο. με
με  φυσική και
φυσική και  ακέραιος
ακέραιος περνοντας
περνοντας έχω
έχω  . Τώρα κάνω αφαίρεση τετραγώνων και επειδή ο μέγιστος κοινός παράγοντας των παρενθέσεων είναι το
. Τώρα κάνω αφαίρεση τετραγώνων και επειδή ο μέγιστος κοινός παράγοντας των παρενθέσεων είναι το  έχω το σύστημα:
έχω το σύστημα:



 θα πρέπει το
θα πρέπει το 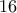 να διαιρεί το
να διαιρεί το  που είναι αδύνατο.
που είναι αδύνατο. έχω τις λύσεις :
έχω τις λύσεις :
 κάνω αφερεση τετράγωνον και επειδή ΜΚΠ των παρενθέσεων είναι το ένα έχω το σύστημα:
κάνω αφερεση τετράγωνον και επειδή ΜΚΠ των παρενθέσεων είναι το ένα έχω το σύστημα:


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες