 με
με  τέτοιοι ώστε:
τέτοιοι ώστε: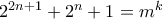
Σχόλιο:Το περίεργο είναι ότι η άσκηση τέθηκε στην Τουρκία το 2003 και στην
 σε ποίο εύκολη μορφή (
σε ποίο εύκολη μορφή ( ) το 2006
) το 2006Συντονιστές: cretanman, silouan, rek2
 με
με  τέτοιοι ώστε:
τέτοιοι ώστε: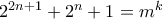
 σε ποίο εύκολη μορφή (
σε ποίο εύκολη μορφή ( ) το 2006
) το 2006 έχω τη λύση
έχω τη λύση 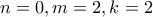 . Για
. Για  είναι άμεσο ότι δεν υπάρχει λύση.
είναι άμεσο ότι δεν υπάρχει λύση. έχω
έχω
 περιττός, τότε
περιττός, τότε  επίσης περιττός. Άρα
επίσης περιττός. Άρα  . Τότε
. Τότε  οπότε
οπότε  .
. είναι άρτιος, έστω
είναι άρτιος, έστω  . Τότε
. Τότε
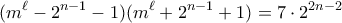

 πρέπει και οι δύο να είναι άρτιοι με τουλάχιστον τον ένα από τους δύο να μην είναι πολλαπλάσιος του
πρέπει και οι δύο να είναι άρτιοι με τουλάχιστον τον ένα από τους δύο να μην είναι πολλαπλάσιος του  . Πρέπει λοιπόν να έχουμε μια από τις πιο κάτω περιπτώσεις:
. Πρέπει λοιπόν να έχουμε μια από τις πιο κάτω περιπτώσεις: και
και 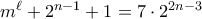
 και
και 
 και
και 
 που είναι άτοπο αφού δίνει
που είναι άτοπο αφού δίνει  .
. . Για
. Για 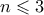 το δεξί μέλος είναι μικρότερο του
το δεξί μέλος είναι μικρότερο του  , άτοπο. Για
, άτοπο. Για  παίρνουμε
παίρνουμε  που δίνει τη λύση
που δίνει τη λύση  . Για
. Για 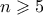 έχουμε
έχουμε  που δίνει
που δίνει  , άτοπο.
, άτοπο. . Για να είναι το δεξί μέλος θετικό πρέπει
. Για να είναι το δεξί μέλος θετικό πρέπει  ή
ή  που εύκολα απορρίπτονται.
που εύκολα απορρίπτονται. και
και 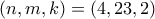 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες