 . Να βρεθεί το πλήθος των μη αρνητικών ακεραίων
. Να βρεθεί το πλήθος των μη αρνητικών ακεραίων  οι οποίοι είναι μικρότεροι ή ίσοι του
οι οποίοι είναι μικρότεροι ή ίσοι του  και ικανοποιούν τις ακόλουθες ιδιότητες:
και ικανοποιούν τις ακόλουθες ιδιότητες:(α) Ο
 είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  .
.(β) Κάθε δεκαδικό ψηφίο του
 είναι ένα από τα
είναι ένα από τα  και
και  .
.Συντονιστές: Demetres, silouan
 . Να βρεθεί το πλήθος των μη αρνητικών ακεραίων
. Να βρεθεί το πλήθος των μη αρνητικών ακεραίων  οι οποίοι είναι μικρότεροι ή ίσοι του
οι οποίοι είναι μικρότεροι ή ίσοι του  και ικανοποιούν τις ακόλουθες ιδιότητες:
και ικανοποιούν τις ακόλουθες ιδιότητες: είναι πολλαπλάσιο του
είναι πολλαπλάσιο του  .
. είναι ένα από τα
είναι ένα από τα  και
και  .
. δεν είναι πολλαπλάσιο του
δεν είναι πολλαπλάσιο του  , θεωρούμε απλώς τους
, θεωρούμε απλώς τους  -ψήφιους αριθμούς (όπου το
-ψήφιους αριθμούς (όπου το  θεωρείται πιθανό εξ αριστερών ψηφίο).
θεωρείται πιθανό εξ αριστερών ψηφίο). ) ψηφία ισότιμα με
) ψηφία ισότιμα με  (
( ή
ή  ) και ισότιμα με
) και ισότιμα με  (
( ). Αν ο αριθμός των ψηφίων modulo
). Αν ο αριθμός των ψηφίων modulo  είναι
είναι  και αυτών modulo
και αυτών modulo  είναι
είναι  , τότε έχουμε
, τότε έχουμε  δυνατότητες (από επιλογή θέσεων και ψηφίου modulo
δυνατότητες (από επιλογή θέσεων και ψηφίου modulo  , αφού έχουμε μόνο ένα ψηφίο ισότιμο με
, αφού έχουμε μόνο ένα ψηφίο ισότιμο με  modulo
modulo  ) και συνολικά οι συνδυασμοί είναι
) και συνολικά οι συνδυασμοί είναι  .
.![\displaystyle \sum_{n} \binom{k}{m + 3n} = \frac{2}{3} \left[2^{k-1} + \cos \left( \frac{\pi (k - 2m)}{3} \right) \right] \displaystyle \sum_{n} \binom{k}{m + 3n} = \frac{2}{3} \left[2^{k-1} + \cos \left( \frac{\pi (k - 2m)}{3} \right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/d92e0ad420bafd39fdfe1883b6def39c.png)
![\displaystyle \frac{1}{3} \sum_m 2^m \binom{k}{m} \left[2^{k-m} + 2 \cos \left( \frac{\pi (k - 3m)}{3} \right) \right] = \frac{2^k}{3} \sum_m \binom{k}{m} + \frac{2}{3} \cos \left( \frac{\pi k}{3} \right) \sum_m (-2)^m \binom{k}{m} = \displaystyle \frac{1}{3} \sum_m 2^m \binom{k}{m} \left[2^{k-m} + 2 \cos \left( \frac{\pi (k - 3m)}{3} \right) \right] = \frac{2^k}{3} \sum_m \binom{k}{m} + \frac{2}{3} \cos \left( \frac{\pi k}{3} \right) \sum_m (-2)^m \binom{k}{m} =](/forum/ext/geomar/texintegr/latexrender/pictures/535abafb4cff7fa339d61f8e89c4a2f6.png)
![\displaystyle = \frac{2}{3} \left[ 2^{2k-1} + \cos \left( \frac{4 \pi k}{3} \right) \right] \displaystyle = \frac{2}{3} \left[ 2^{2k-1} + \cos \left( \frac{4 \pi k}{3} \right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/53e7e36280d6e0940fa55615492794b9.png)
Ας δούμε και την απόδειξη μιας και δεν νομίζω να θυμόμαστε την ταυτότητα εν ώρα διαγωνισμού:dement έγραψε: Ισχύει (ταυτότητα) ότι![\displaystyle \sum_{n} \binom{k}{m + 3n} = \frac{2}{3} \left[2^{k-1} + \cos \left( \frac{\pi (k - 2m)}{3} \right) \right] \displaystyle \sum_{n} \binom{k}{m + 3n} = \frac{2}{3} \left[2^{k-1} + \cos \left( \frac{\pi (k - 2m)}{3} \right) \right]](/forum/ext/geomar/texintegr/latexrender/pictures/d92e0ad420bafd39fdfe1883b6def39c.png)

 , όπου
, όπου  και προσθέτουμε.
και προσθέτουμε.  είναι
είναι  ενώ για
ενώ για  είναι
είναι  . Άρα παίρνουμε
. Άρα παίρνουμε![\displaystyle{ 2^n + (1+\omega)^n + (1+\omega^2)^n = 3\left[\binom{n}{0} + \binom{n}{3} + \cdots \right]} \displaystyle{ 2^n + (1+\omega)^n + (1+\omega^2)^n = 3\left[\binom{n}{0} + \binom{n}{3} + \cdots \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/e40edfa55643a3040c7e76c273552ff9.png)
![\begin{aligned}
\binom{n}{0} + \binom{n}{3} + \cdots &= \frac{1}{3}\left[ 2^n + (1+\omega)^n + (1+\omega^2)^n \right] \\
&= \frac{1}{3}\left[ 2^n + (-\omega^2)^n + (-\omega)^n \right] \\
&= \frac{1}{3}\left[2^n + (-1)^n(\omega^n + \omega^{2n})\right] \\
&= \begin{cases}
\frac{1}{3}\left[2^n + 2(-1)^n\right] & n\equiv 0 \bmod 3 \\
\frac{1}{3}\left[2^n + (-1)^{n+1}\right] & n \not \equiv 0 \bmod 3
\end{cases}
\end{aligned} \begin{aligned}
\binom{n}{0} + \binom{n}{3} + \cdots &= \frac{1}{3}\left[ 2^n + (1+\omega)^n + (1+\omega^2)^n \right] \\
&= \frac{1}{3}\left[ 2^n + (-\omega^2)^n + (-\omega)^n \right] \\
&= \frac{1}{3}\left[2^n + (-1)^n(\omega^n + \omega^{2n})\right] \\
&= \begin{cases}
\frac{1}{3}\left[2^n + 2(-1)^n\right] & n\equiv 0 \bmod 3 \\
\frac{1}{3}\left[2^n + (-1)^{n+1}\right] & n \not \equiv 0 \bmod 3
\end{cases}
\end{aligned}](/forum/ext/geomar/texintegr/latexrender/pictures/3a23ceb8dcb1b58d6d3e1a13e4af8db5.png)
 και
και  αντίστοιχα.] Μπορούμε επίσης να χρησιμοποιήσουμε και συμμετρία. Π.χ. αν
αντίστοιχα.] Μπορούμε επίσης να χρησιμοποιήσουμε και συμμετρία. Π.χ. αν 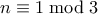 είναι
είναι 
 για το πλήθος των
για το πλήθος των  που ικανοποιούν το (β) αλλά είναι ισότιμα με
που ικανοποιούν το (β) αλλά είναι ισότιμα με  και
και  αντίστοιχα. Είναι άμεσο ότι
αντίστοιχα. Είναι άμεσο ότι 


 και
και  .
. 



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες