Σταύρο, αυτή είναι ουσιαστικά και η δική μου λύση. Μπορούμε να την μετατρέψουμε και σε λύση εντός φακέλου.
Τοποθετούμε τον πρώτο κύκλο πάνω στον δεύτερο με οποιοδήποτε τρόπο. Για κάθε σημαδεμένο σημείο

του πρώτου κύκλου ορίζουμε το σύνολο

ως το σύνολο όλων των

, ώστε αν περιστρέψουμε τον πρώτο κύκλο ωρολογιακά κατά γωνία

, το σημείο

θα καταλήξει σε ένα από τα μπλε τόξα.
Κάθε μπλε τόξο μήκους

, αντιστοιχεί με αυτόν τον τρόπο σε ένα διάστημα του
![[0,2\pi] [0,2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png)
μήκους

. Δηλαδή το

είναι ένωση διαστημάτων συνολικού μήκους μικρότερου του

. Άρα η ένωση όλων των

για κάθε σημαδεμένο σημείο

, είναι και αυτή ένωση διαστημάτων συνολικού μήκους μικρότερου του
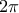
. Δηλαδή υπάρχει στοιχείο

του
![[0,2\pi] [0,2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png)
το οποίο δεν ανήκει σε κανένα από τα

.
Αν λοιπόν περιστρέψουμε τον πρώτο κύκλο κατά γωνία

, τότε κανένα από τα σημαδεμένα σημεία δεν θα ανήκει πάνω σε μπλε τόξο. Κερδίζει δηλαδή ο Γιάννης.
 . Τοποθετούμε στην περιφέρεια του πρώτου
. Τοποθετούμε στην περιφέρεια του πρώτου  "καλά" σημεία και βάφουμε μπλέ μερικά τόξα με άθροισμα μηκών μικρότερο του
"καλά" σημεία και βάφουμε μπλέ μερικά τόξα με άθροισμα μηκών μικρότερο του  στον δεύτερο κύκλο. Στην συνέχεια τοποθετούμε τον ένα κύκλο πάνω στον άλλον. Υπάρχει τοποθέτηση ώστε να μην υφίσταται "καλό" σημείο του πρώτου κύκλου που να βρίσκεται σε μπλε τόξο;
στον δεύτερο κύκλο. Στην συνέχεια τοποθετούμε τον ένα κύκλο πάνω στον άλλον. Υπάρχει τοποθέτηση ώστε να μην υφίσταται "καλό" σημείο του πρώτου κύκλου που να βρίσκεται σε μπλε τόξο;
 που έχει μάζα 1 στα
που έχει μάζα 1 στα  το σύνολο από τα τόξα.
το σύνολο από τα τόξα.
 το μέτρο Lebesgue του
το μέτρο Lebesgue του  ο κύκλος και δεν κερδίζει ο Γιώργος.
ο κύκλος και δεν κερδίζει ο Γιώργος.

 η χαρακτηριστική του
η χαρακτηριστική του 


 με την προυπόθεση το
με την προυπόθεση το  του πρώτου κύκλου ορίζουμε το σύνολο
του πρώτου κύκλου ορίζουμε το σύνολο  ως το σύνολο όλων των
ως το σύνολο όλων των  , ώστε αν περιστρέψουμε τον πρώτο κύκλο ωρολογιακά κατά γωνία
, ώστε αν περιστρέψουμε τον πρώτο κύκλο ωρολογιακά κατά γωνία  , αντιστοιχεί με αυτόν τον τρόπο σε ένα διάστημα του
, αντιστοιχεί με αυτόν τον τρόπο σε ένα διάστημα του ![[0,2\pi] [0,2\pi]](/forum/ext/geomar/texintegr/latexrender/pictures/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png) μήκους
μήκους  . Δηλαδή το
. Δηλαδή το  . Άρα η ένωση όλων των
. Άρα η ένωση όλων των 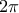 . Δηλαδή υπάρχει στοιχείο
. Δηλαδή υπάρχει στοιχείο  του
του