Παρατηρούμε ότι το άθροισμα

όλων των βαθμών οφείλει να είναι άρτιος: αυτό προκύπτει από την

και την συνεπαγόμενη διαιρετότητα του

δια του

. (Ο

οφείλει να είναι πολλαπλάσιο του

λόγω της

, οπότε θέτοντας

συμπεραίνουμε ότι ο

οφείλει να είναι ακέραιος, άρα

.)
Αν δεν μπορούμε να διαχωρίσουμε το σύνολο των μαθητών σε δύο υποομάδες με

μαθητές η κάθε μία και ίσο άθροισμα βαθμών (άρα και μέσο όρο

η κάθε μία), τότε υπάρχει μία ελάχιστη δυνατή διαφορά

ανάμεσα σε δύο πλησιέστερες βαθμολογικά υποομάδες ... και, επειδή το άθροισμα όλων των βαθμών είναι άρτιος,

. Ας είναι λοιπόν

,

τα αθροίσματα βαθμών των δύο υποομάδων μαθητών, με

.
Αν υπάρχει 10 στην υποομάδα (με άθροισμα βαθμών)

, τότε δεν μπορεί να υπάρχει 9 στην υποομάδα (με άθροισμα βαθμών)

, καθώς σε μια τέτοια περίπτωση στέλνουμε το 10 της

στην

και το 9 της

στην

και μικραίνουμε κατά

την διαφορά ανάμεσα στις

και

, κάτι αδύνατον κάτω από τις ως τώρα παραδοχές μας. (Αν

τότε δημιουργούνται δύο υποομάδες με ίσες συνολικές βαθμολογίες, ενώ αν

τότε δημιουργούνται δύο υποομάδες με διαφορά συνολικών βαθμολογιών μικρότερη του

.) Αν λοιπόν υπάρχει 10 στην

τότε όλα τα 9 βρίσκονται επίσης στην

. Με ανάλογο συλλογισμό στην

βρίσκονται και όλα τα 8, αλλά και όλα τα 7, κοκ Έχουμε καταλήξει σε άτοπο υποθέτοντας ότι στην υποομάδα

υπάρχει μαθητής με βαθμό 10. Αναλόγως δεν μπορεί να υπάρχει μαθητής με βαθμό 9 στην

, διότι τότε η

οφείλει να περιέχει όλους τους βαθμούς από 8 και κάτω, κοκ
[Στον παραπάνω δια της εις άτοπον απαγωγής συλλογισμό χρησιμοποιήθηκε η υπόθεση ότι κάθε βαθμός εμφανίζεται μία τουλάχιστον φορά ... στην κατά

κάθοδο σε κάθε βήμα. Για ένα αντιπαράδειγμα ας θεωρήσουμε μία τάξη

μαθητών με βαθμούς 9, 9, 9, 9, 9, 9, 9, 5, 3, 3.]
 δόθηκε ένα διαγώνισμα όπου οι δυνατές βαθμολογίες ήταν οι
δόθηκε ένα διαγώνισμα όπου οι δυνατές βαθμολογίες ήταν οι  Κάθε μία από αυτές τις βαθμολογίες εμφανίστηκε τουλάχιστον μία φορά. Η μέση βαθμολογία ήταν ακριβώς
Κάθε μία από αυτές τις βαθμολογίες εμφανίστηκε τουλάχιστον μία φορά. Η μέση βαθμολογία ήταν ακριβώς  Να δειχθεί ότι μπορούμε να χωρίσουμε τους μαθητές της τάξης σε δύο ίσες ομάδες των
Να δειχθεί ότι μπορούμε να χωρίσουμε τους μαθητές της τάξης σε δύο ίσες ομάδες των  μαθητών με τέτοιο τρόπο ώστε στην κάθε ομάδα η μέση βαθμολογία να είναι ακριβώς
μαθητών με τέτοιο τρόπο ώστε στην κάθε ομάδα η μέση βαθμολογία να είναι ακριβώς 

 όλων των βαθμών οφείλει να είναι άρτιος: αυτό προκύπτει από την
όλων των βαθμών οφείλει να είναι άρτιος: αυτό προκύπτει από την  και την συνεπαγόμενη διαιρετότητα του
και την συνεπαγόμενη διαιρετότητα του  . (Ο
. (Ο  , οπότε θέτοντας
, οπότε θέτοντας  συμπεραίνουμε ότι ο
συμπεραίνουμε ότι ο  οφείλει να είναι ακέραιος, άρα
οφείλει να είναι ακέραιος, άρα  .)
.) η κάθε μία), τότε υπάρχει μία ελάχιστη δυνατή διαφορά
η κάθε μία), τότε υπάρχει μία ελάχιστη δυνατή διαφορά  ανάμεσα σε δύο πλησιέστερες βαθμολογικά υποομάδες ... και, επειδή το άθροισμα όλων των βαθμών είναι άρτιος,
ανάμεσα σε δύο πλησιέστερες βαθμολογικά υποομάδες ... και, επειδή το άθροισμα όλων των βαθμών είναι άρτιος,  . Ας είναι λοιπόν
. Ας είναι λοιπόν  ,
,  τα αθροίσματα βαθμών των δύο υποομάδων μαθητών, με
τα αθροίσματα βαθμών των δύο υποομάδων μαθητών, με  .
.  την διαφορά ανάμεσα στις
την διαφορά ανάμεσα στις  τότε δημιουργούνται δύο υποομάδες με ίσες συνολικές βαθμολογίες, ενώ αν
τότε δημιουργούνται δύο υποομάδες με ίσες συνολικές βαθμολογίες, ενώ αν  τότε δημιουργούνται δύο υποομάδες με διαφορά συνολικών βαθμολογιών μικρότερη του
τότε δημιουργούνται δύο υποομάδες με διαφορά συνολικών βαθμολογιών μικρότερη του  κάθοδο σε κάθε βήμα. Για ένα αντιπαράδειγμα ας θεωρήσουμε μία τάξη
κάθοδο σε κάθε βήμα. Για ένα αντιπαράδειγμα ας θεωρήσουμε μία τάξη  μαθητών με βαθμούς 9, 9, 9, 9, 9, 9, 9, 5, 3, 3.]
μαθητών με βαθμούς 9, 9, 9, 9, 9, 9, 9, 5, 3, 3.] (και άθροισμα
(και άθροισμα  ) έκαστη: αναφερόμενος τώρα στον συλλογισμό που εφαρμόστηκε στην περίπτωση των ΕΝΔΕΚΑ βαθμών, θα μπορούσα να θεωρήσω
) έκαστη: αναφερόμενος τώρα στον συλλογισμό που εφαρμόστηκε στην περίπτωση των ΕΝΔΕΚΑ βαθμών, θα μπορούσα να θεωρήσω  ,
,  , και να παρατηρήσω ότι μετά το 6 της
, και να παρατηρήσω ότι μετά το 6 της  : το πρόβλημα είναι ότι υπάρχει ήδη άλλος διαμερισμός με
: το πρόβλημα είναι ότι υπάρχει ήδη άλλος διαμερισμός με  , κλπ κλπ (Βλέπουμε δηλαδή ότι η ύπαρξη τριών διαδοχικών βαθμών, που εξασφαλίζεται από το πλήθος των υπαρκτών βαθμών (ΕΠΤΑ) στο σύνολο των δυνατών ΕΝΔΕΚΑ βαθμών (μέσω της αρχής της περιστερότρυπας), αφ' ενός μεν δεν σώζει τον συλλογισμό που εφαρμόστηκε στην περίπτωση του αρχικού προβλήματος, αφ' ετέρου δε επιτρέπει τον διαμερισμό σε δύο ισοπληθείς και βαθμολογικά ίσες υποομάδες.)
, κλπ κλπ (Βλέπουμε δηλαδή ότι η ύπαρξη τριών διαδοχικών βαθμών, που εξασφαλίζεται από το πλήθος των υπαρκτών βαθμών (ΕΠΤΑ) στο σύνολο των δυνατών ΕΝΔΕΚΑ βαθμών (μέσω της αρχής της περιστερότρυπας), αφ' ενός μεν δεν σώζει τον συλλογισμό που εφαρμόστηκε στην περίπτωση του αρχικού προβλήματος, αφ' ετέρου δε επιτρέπει τον διαμερισμό σε δύο ισοπληθείς και βαθμολογικά ίσες υποομάδες.) . Βεβαίως ο αριθμός εμφανίσεων του
. Βεβαίως ο αριθμός εμφανίσεων του  } (όπου όμως η Εικασία 7/11 ισχύει λόγω της
} (όπου όμως η Εικασία 7/11 ισχύει λόγω της  ) και {
) και { } (όπου η Εικασία 7/11 ισχύει και πάλι λόγω της
} (όπου η Εικασία 7/11 ισχύει και πάλι λόγω της  ). (Επισημαίνω και κάτι μάλλον προφανές: στις υπόλοιπες 13 περιπτώσεις άλλοτε υπάρχει λύση με κάθε υποομάδα να περιέχει ακριβώς ένα
). (Επισημαίνω και κάτι μάλλον προφανές: στις υπόλοιπες 13 περιπτώσεις άλλοτε υπάρχει λύση με κάθε υποομάδα να περιέχει ακριβώς ένα  ,
, 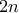 }, για παράδειγμα).]
}, για παράδειγμα).] (ελάχιστο δυνατό) έχουμε ήδη το αντιπαράδειγμα {
(ελάχιστο δυνατό) έχουμε ήδη το αντιπαράδειγμα { } ... που πάντως είναι το μόνο δυνατό στην κατηγορία του*.
} ... που πάντως είναι το μόνο δυνατό στην κατηγορία του*. (αρχική εικασία 7/11) είναι απλώς θέμα χρόνου και προσπάθειας ... χωρίς φυσικά να αποκλείεται η πιθανότητα εκπλήξεων, μεγαλύτερου 'βάθους' του προβλήματος, κλπ κλπ
(αρχική εικασία 7/11) είναι απλώς θέμα χρόνου και προσπάθειας ... χωρίς φυσικά να αποκλείεται η πιθανότητα εκπλήξεων, μεγαλύτερου 'βάθους' του προβλήματος, κλπ κλπ  }, {
}, { }, {
}, { }, {
}, { }, {
}, { }, {
}, { }, {
}, { }, {
}, { }, {
}, { }, {
}, { }, {
}, { }, {
}, { }, {
}, { }.
}. και για
και για  βρίσκω ανάλογα αντιπαραδείγματα, {
βρίσκω ανάλογα αντιπαραδείγματα, { } και {
} και { }
}  . Το συνολικό άθροισμα είναι
. Το συνολικό άθροισμα είναι  οπότε κάθε υποσύνολο θα έπρεπε να έχει άθροισμα
οπότε κάθε υποσύνολο θα έπρεπε να έχει άθροισμα  . Κάθε υποσύνολο θα έχει
. Κάθε υποσύνολο θα έχει  αριθμούς. Άρα ένα από αυτά θα έχει τουλάχιστον
αριθμούς. Άρα ένα από αυτά θα έχει τουλάχιστον  και άρα άθροισμα τουλάχιστον
και άρα άθροισμα τουλάχιστον  , άτοπο.
, άτοπο. .
. ) αλλά δεν το βρήκα ... και όσο δεν το έβρισκα ... τόσο υποπτευόμουν και εγώ κάτι καλό για μεγάλα
) αλλά δεν το βρήκα ... και όσο δεν το έβρισκα ... τόσο υποπτευόμουν και εγώ κάτι καλό για μεγάλα  , ...) όπου
, ...) όπου  από τους
από τους  αριθμούς {
αριθμούς { } εμφανίζονται μία ή δύο φορές ο καθένας (με τέτοιο τρόπο ώστε και το πλήθος και το άθροισμα τους να είναι άρτιο).]
} εμφανίζονται μία ή δύο φορές ο καθένας (με τέτοιο τρόπο ώστε και το πλήθος και το άθροισμα τους να είναι άρτιο).] , από εκεί και πέρα η αναζήτηση χωρίς κάποιες νέες ιδέες θα ήταν απαγορευτικά χρονοβόρα.
, από εκεί και πέρα η αναζήτηση χωρίς κάποιες νέες ιδέες θα ήταν απαγορευτικά χρονοβόρα. ).) Έτσι μπορούμε να πούμε ότι είχα ουσιαστικά βρει όλα τα αντιπαραδείγματα για
).) Έτσι μπορούμε να πούμε ότι είχα ουσιαστικά βρει όλα τα αντιπαραδείγματα για  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
.