Θα αποδείξουμε πρώτα ότι ισχύει

.
Προς άτοπο, έστω ότι γίνεται

, και έστω

το κοινό πλήθος νομισμάτων των κουμπαράδων αυτών.
Έστω

τα νομίσματα που περιέχουν οι

κουμπαράδες.
Για
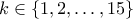
, ορίζουμε

(π.χ.

).
Εύκολα παρατηρούμε ότι όλα τα

είναι ίσα μεταξύ τους. Π.χ.

γιατί αν προσθέσουμε ένα νόμισμα στον κουμπαρά με πλήθος νομισμάτων π.χ.

, στην 15-άδα που διαλέξαμε ανήκει ή ο
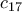
ή ο

, οπότε κάθε φορά που προστίθεται νόμισμα στο

, προστίθεται και στο

, ό.έ.δ.
Ορίζουμε έναν κουμπαρά ως
καλό, αν έχει πλήθος νομισμάτων

.
Καταρχήν παρατηρούμε ότι τα αθροίσματα

, με

έχουν

προσθετέους, ενώ τα αθροίσματα

, με
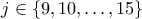
έχουν

προσθετέους.
Θα αποδείξουμε το εξής Λήμμα:
Λήμμα
Υπάρχουν δείκτες

ώστε στα αθροίσματα

όλοι οι προσθετέοι είναι καλοί κουμπαράδες.
Θα δειχτεί πρώτα το εξής Λήμμα 1 (ως μέρος της απόδειξης του Λήμματος πιο πάνω):
Λήμμα 1
Σε ένα τουλάχιστον εκ των

, με
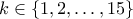
όλοι οι προσθετέοι είναι καλοί κουμπαράδες.
Απόδειξη
Αν σε κανένα εκ των

όλοι οι προσθετέοι δεν είναι καλοί, τότε το μέγιστο πλήθος των καλών κουμπαράδων είναι το πολύ
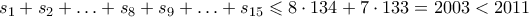
, άτοπο, οπότε το Λήμμα 1 αποδείχτηκε.
Έστω λοιπόν ότι ο κουμπαράς

έχει όλα τα στοιχεία του καλά. Με την διαδικασία του Λήμματος 1, δείχνουμε ότι τουλάχιστον

ακόμη εκ των

πρέπει να έχουν όλα τα στοιχεία τους καλά. Αν τώρα κάποιος εκ των

έχει τα στοιχεία του καλά, το αρχικό Λήμμα αποδείχτηκε. Αν όχι, τότε όλοι οι
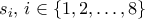
πρέπει να έχουν όλα τα στοιχεία τους καλά. Πάλι, όμως, μένει ένα ακόμη

που πρέπει να έχει όλα τα στοιχεία του καλά, και προφανώς αυτό ανήκει στα

Έστω λοιπόν
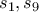
τα δύο αυτά αθροίσματα, με όλους τους προσθετέους να είναι καλοί κουμπαράδες.
Το

είναι άθροισμα

καλών κουμπαράδων, με καθένα τιμή

.
Το

είναι άθροισμα

καλών κουμπαράδων, με καθένα τιμή

.
Τότε, αφού

, όπως δείχτηκε στην αρχή, είναι

, άτοπο.
Επομένως,

.
Για

πραγματοποιούμε την εξής κατασκευή :
Για

, επιλέγουμε τους

.
Επίσης, επιλέγουμε τους Νο -

κουμπαράδες.
Έτσι , κάθε ένας εκ των κουμπαράδων

έχει ένα νόμισμα, άρα επιτυγχάνεται η τιμή

.
Τελικά,
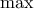

.
 κουμπαράδες. Κάθε μέρα, ο Δημήτρης επιλέγει
κουμπαράδες. Κάθε μέρα, ο Δημήτρης επιλέγει  διαδοχικούς κουμπαράδες και βάζει σε κάθε ένα από αυτούς από ένα νόμισμα.
διαδοχικούς κουμπαράδες και βάζει σε κάθε ένα από αυτούς από ένα νόμισμα.  κουμπαράδες, όχι απαραίτητα διαδοχικοί, που περιέχουν τον ίδιο (θετικό) αριθμό νομισμάτων.
κουμπαράδες, όχι απαραίτητα διαδοχικοί, που περιέχουν τον ίδιο (θετικό) αριθμό νομισμάτων.  ;
;
 .
. , και έστω
, και έστω  το κοινό πλήθος νομισμάτων των κουμπαράδων αυτών.
το κοινό πλήθος νομισμάτων των κουμπαράδων αυτών. τα νομίσματα που περιέχουν οι
τα νομίσματα που περιέχουν οι 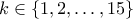 , ορίζουμε
, ορίζουμε  (π.χ.
(π.χ.  ).
). είναι ίσα μεταξύ τους. Π.χ.
είναι ίσα μεταξύ τους. Π.χ.  γιατί αν προσθέσουμε ένα νόμισμα στον κουμπαρά με πλήθος νομισμάτων π.χ.
γιατί αν προσθέσουμε ένα νόμισμα στον κουμπαρά με πλήθος νομισμάτων π.χ.  , στην 15-άδα που διαλέξαμε ανήκει ή ο
, στην 15-άδα που διαλέξαμε ανήκει ή ο 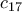 ή ο
ή ο  , οπότε κάθε φορά που προστίθεται νόμισμα στο
, οπότε κάθε φορά που προστίθεται νόμισμα στο  , προστίθεται και στο
, προστίθεται και στο  , ό.έ.δ.
, ό.έ.δ. , με
, με  έχουν
έχουν  προσθετέους, ενώ τα αθροίσματα
προσθετέους, ενώ τα αθροίσματα  , με
, με 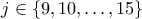 έχουν
έχουν  προσθετέους.
προσθετέους. ώστε στα αθροίσματα
ώστε στα αθροίσματα  όλοι οι προσθετέοι είναι καλοί κουμπαράδες.
όλοι οι προσθετέοι είναι καλοί κουμπαράδες. , με
, με 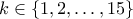 όλοι οι προσθετέοι είναι καλοί κουμπαράδες.
όλοι οι προσθετέοι είναι καλοί κουμπαράδες.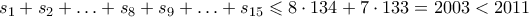 , άτοπο, οπότε το Λήμμα 1 αποδείχτηκε.
, άτοπο, οπότε το Λήμμα 1 αποδείχτηκε. ακόμη εκ των
ακόμη εκ των 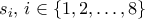 πρέπει να έχουν όλα τα στοιχεία τους καλά. Πάλι, όμως, μένει ένα ακόμη
πρέπει να έχουν όλα τα στοιχεία τους καλά. Πάλι, όμως, μένει ένα ακόμη 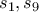 τα δύο αυτά αθροίσματα, με όλους τους προσθετέους να είναι καλοί κουμπαράδες.
τα δύο αυτά αθροίσματα, με όλους τους προσθετέους να είναι καλοί κουμπαράδες.  είναι άθροισμα
είναι άθροισμα  , όπως δείχτηκε στην αρχή, είναι
, όπως δείχτηκε στην αρχή, είναι  , άτοπο.
, άτοπο. .
. πραγματοποιούμε την εξής κατασκευή :
πραγματοποιούμε την εξής κατασκευή : , επιλέγουμε τους
, επιλέγουμε τους  .
. κουμπαράδες.
κουμπαράδες.  έχει ένα νόμισμα, άρα επιτυγχάνεται η τιμή
έχει ένα νόμισμα, άρα επιτυγχάνεται η τιμή 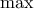
 , ένα εκ των
, ένα εκ των  ένα εκ των
ένα εκ των  . Ξεκινώντας από την πρώτη 15άδα την πρώτη μέρα (Νο 1 - Νο15) την δεύτερη 15άδα την δεύτερη μέρα κοκ, μετά από 134 μέρες θα έχουμε
. Ξεκινώντας από την πρώτη 15άδα την πρώτη μέρα (Νο 1 - Νο15) την δεύτερη 15άδα την δεύτερη μέρα κοκ, μετά από 134 μέρες θα έχουμε  κουμπαράδες στην σιερά με ένα νόμισμα έκαστος. Την επόμενη ημέρα τοποθετούμε από ένα νόμισμα στους 15 τελευταίους κουμπαράδες (Νο2004 ως Νο2018). Τότε 7 κουμπαράδες (Νο 2004 ως και Νο2010) θα έχουν 2 νομίσματα και οι υπόλοιποι 2011 από 1. Αρα υπάρχει
κουμπαράδες στην σιερά με ένα νόμισμα έκαστος. Την επόμενη ημέρα τοποθετούμε από ένα νόμισμα στους 15 τελευταίους κουμπαράδες (Νο2004 ως Νο2018). Τότε 7 κουμπαράδες (Νο 2004 ως και Νο2010) θα έχουν 2 νομίσματα και οι υπόλοιποι 2011 από 1. Αρα υπάρχει