Ωραία άσκηση. Από που είναι;
Θα δείξουμε ότι υπάρχει τέτοιος πίνακας αν και μόνο αν

ή

άρτιος.
Αν

προφανώς υπάρχει τέτοιος πίνακας.
Αν
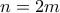
άρτιος θα δείξουμε με κατασκευή ότι γίνεται: Ξεκινάμε από την δεύτερη σειρά και γράφουμε τους πρώτους

αριθμούς από αριστερά στα δεξιά (μένει η τελευταία θέση κενή). Μετά τους επόμενους

αριθμούς στην τρίτη σειρά από δεξιά προς τα αριστερά. (Ξεκινώντας από την τελευταία θέση και τελειώνοντας στην πρώτη.) Συνεχίζουμε έτσι εναλλάξ μέχρι να συμπληρώσουμε και τους πρώτους

αριθμούς της τελευταίας σειράς. Επειδή

άρτιος αυτή θα είναι η

φορά (περιττός αριθμός) που συμπληρώνουμε μια σειρά και η συμπλήρωση θα γίνει από αριστερά προς δεξιά. Τώρα συμπληρώνουμε τους αριθμούς

ως

στην τελευταία στήλη από κάτω προς τα πάνω και τέλος τους υπόλοιπους

αριθμούς στην πρώτη σειρά από δεξιά προς τα αριστερά.
Ας συγκρίνουμε τους αριθμούς που βρίσκονται στη στήλη

όταν μετακινηθούμε από τη στήλη

στη στήλη

. Ας υποθέσουμε πρώτα ότι

και

Αν

άρτιος θα έχουμε αύξηση κατά

.
Αν

περιττός θα έχουμε αύξηση κατά

.
Είναι εύκολο να ελεγχθεί ότι οι πιο πάνω τύποι ισχύουν και για

. Παρατηρούμε επίσης ότι από τη στήλη

στη στήλη

η αύξηση είναι

ανεξαρτήτως του

. Επειδή στην πρώτη σειρά όλοι οι αριθμοί είναι διαφορετικοί

, το ίδιο θα ισχύει και σε κάθε άλλη περιττή σειρά. Το ίδιο ισχύει και για τις άρτιες σειρές αφού είναι απλό ότι και η δεύτερη σειρά έχει όλους τους αριθμούς διαφορετικούς modulo

.
Αν

περιττός με
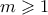
θα δείξουμε με άτοπο ότι τέτοιος πίνακας δεν υπάρχει. Κοιτάζουμε που τοποθετήθηκαν οι αριθμοί που είναι ισότιμοι με

και

modulo

. Για κάθε υπόλοιπο θα έχουμε από ένα σε κάθε σειρά και κάθε στήλη. Επίσης οι αριθμοί μπορούν να χωριστούν σε

γειτονικά ζευγάρια. Έστω ότι

από τα ζευγάρια είναι οριζόντια και

είναι κάθετα. Αφού

περιττός μπορούμε χωρίς βλάβης της γενικότητας να υποθέσουμε ότι και ο

είναι περιττός.
Μένει να δείξουμε ότι και οι αριθμοί στης στήλες είναι διαφορετικοί

. Έστω προς άτοπο ότι έχουμε στη στήλη

δυο ισότιμους αριθμούς, έστω στις σειρές

και

. Ας τους ονομάσουμε

και

. Είναι άμεσο από την κατασκευή ότι

και

. Επειδή

άρτιος, τότε

. Τότε όμως αν π.χ.

, από τα πιο πάνω θα έχουμε

.
Η απόδειξη ότι η κατασκευή είναι σωστή έχει ολοκληρωθεί.
Επειδή στις

στήλες που μπήκαν τα κάθετα ζευγάρια δεν μπορούν να μπουν άλλα ίδια υπόλοιπα, τα

οριζόντια ζευγάρια πρέπει να διαμοιραστούν στις υπόλοιπες

στήλες. Κοιτάζουμε την πρώτη από αριστερά από αυτές τις

στήλες. Έχει ένα υπόλοιπο ισότιμο με

και ένα ισότιμο με

. Αυτά πρέπει να είναι σε ζεύγη με ένα υπόλοιπο ισότιμο με

και ένα ισότιμο με

αντίστοιχα, τα οποία αναγκαστικά θα βρίσκονται στη δεύτερη από αριστερά στήλη. Ομοίως αυτά της τρίτης θα τα αντιστοιχίσουμε σε αυτά της τέταρτης κ.ο.κ. Επειδή όμως

περιττός θα μείνει μια στήλη χωρίς αντιστοιχία, άτοπο.
 Τελβκολ αν μπορούμε να τοποθετήσουμε κάθε έναν από τους ακέραιους
Τελβκολ αν μπορούμε να τοποθετήσουμε κάθε έναν από τους ακέραιους  σε ένα ακριβώς κελι του πίνακα ώστε κάθε ζεύγος διαδοχικών να βρίσκεται σε
σε ένα ακριβώς κελι του πίνακα ώστε κάθε ζεύγος διαδοχικών να βρίσκεται σε  γειτονικά κελιά και το
γειτονικά κελιά και το  να μην διαιρεί καμία διαφορά δύο αριθμών που βρίσκονται στην ίδια γραμμή ή στήλη. Να βρεθεί για ποια
να μην διαιρεί καμία διαφορά δύο αριθμών που βρίσκονται στην ίδια γραμμή ή στήλη. Να βρεθεί για ποια  έχουμε πίνακα Τελβκολ.
έχουμε πίνακα Τελβκολ.
 ή
ή 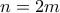 άρτιος θα δείξουμε με κατασκευή ότι γίνεται: Ξεκινάμε από την δεύτερη σειρά και γράφουμε τους πρώτους
άρτιος θα δείξουμε με κατασκευή ότι γίνεται: Ξεκινάμε από την δεύτερη σειρά και γράφουμε τους πρώτους  αριθμούς από αριστερά στα δεξιά (μένει η τελευταία θέση κενή). Μετά τους επόμενους
αριθμούς από αριστερά στα δεξιά (μένει η τελευταία θέση κενή). Μετά τους επόμενους  ως
ως  στην τελευταία στήλη από κάτω προς τα πάνω και τέλος τους υπόλοιπους
στην τελευταία στήλη από κάτω προς τα πάνω και τέλος τους υπόλοιπους  όταν μετακινηθούμε από τη στήλη
όταν μετακινηθούμε από τη στήλη  . Ας υποθέσουμε πρώτα ότι
. Ας υποθέσουμε πρώτα ότι  και
και 
 .
. .
. . Παρατηρούμε επίσης ότι από τη στήλη
. Παρατηρούμε επίσης ότι από τη στήλη  η αύξηση είναι
η αύξηση είναι  ανεξαρτήτως του
ανεξαρτήτως του  . Επειδή στην πρώτη σειρά όλοι οι αριθμοί είναι διαφορετικοί
. Επειδή στην πρώτη σειρά όλοι οι αριθμοί είναι διαφορετικοί  , το ίδιο θα ισχύει και σε κάθε άλλη περιττή σειρά. Το ίδιο ισχύει και για τις άρτιες σειρές αφού είναι απλό ότι και η δεύτερη σειρά έχει όλους τους αριθμούς διαφορετικούς modulo
, το ίδιο θα ισχύει και σε κάθε άλλη περιττή σειρά. Το ίδιο ισχύει και για τις άρτιες σειρές αφού είναι απλό ότι και η δεύτερη σειρά έχει όλους τους αριθμούς διαφορετικούς modulo  περιττός με
περιττός με 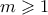 θα δείξουμε με άτοπο ότι τέτοιος πίνακας δεν υπάρχει. Κοιτάζουμε που τοποθετήθηκαν οι αριθμοί που είναι ισότιμοι με
θα δείξουμε με άτοπο ότι τέτοιος πίνακας δεν υπάρχει. Κοιτάζουμε που τοποθετήθηκαν οι αριθμοί που είναι ισότιμοι με  και
και  από τα ζευγάρια είναι οριζόντια και
από τα ζευγάρια είναι οριζόντια και  είναι κάθετα. Αφού
είναι κάθετα. Αφού  . Ας τους ονομάσουμε
. Ας τους ονομάσουμε  και
και  . Είναι άμεσο από την κατασκευή ότι
. Είναι άμεσο από την κατασκευή ότι  και
και  . Επειδή
. Επειδή  . Τότε όμως αν π.χ.
. Τότε όμως αν π.χ.  , από τα πιο πάνω θα έχουμε
, από τα πιο πάνω θα έχουμε  .
.  και ένα ισότιμο με
και ένα ισότιμο με  . Αυτά πρέπει να είναι σε ζεύγη με ένα υπόλοιπο ισότιμο με
. Αυτά πρέπει να είναι σε ζεύγη με ένα υπόλοιπο ισότιμο με